AI image generation is getting crazy good

Miscellaneous and Personal Stuff I Must Share
61

The cat is egregiously bad, but most of the others are also bad. The people look like cheap waxworks from a Madame Tussaud knockoff museum. And their eyes are dead. Note especially the X-Files one. Scully looks labotomized and it not looking in the right direction. Mr. Miyagi is looking over Fonzie’s shoulder and isn’t facing him. What are Bill an Ted looking at, anyway? Shouldn’t it be the Doctor?

They aren’t good in any artistic sense. They might be approaching uncanny valley, but they still have a long way to go.

62

Eh, these are usually quick meme prompts to get a smile on social media, not an attempt to fool people into thinking there was an X-Files/Gremlins crossover. Someone could drag this stuff into a local system using ControlNET to manipulate the poses and various ways to make it more photorealistic but that’s not the point. The point is what you can do with casual effort via means available to anyone.

And, as noted, it is pretty impressive how quickly the technology has progressed in just a few years. Is it perfect? Of course not. But going from horses to sedans in three years is pretty neat even if they’re not flying rocket-powered cars yet. Give it three more years

63

For me they are largely a test of the system, see if it knows who x is. Sometimes the answer is yes, sometimes no, sometimes the answer is “I refuse to draw that because I’ve been told not to”. With most subjects it is one try and move on to the next.

64

Does this mean we can no longer accept photo proof of bigfoot? (or any cryptid?)

65

We never could. There have always been fake photos (and video) of them.

66

That was bit tongue and cheek, but still the previous fake photos screamed fake. Now with AI, presumably they would look more ‘real’.

Note that I don’t believe in BF, so, to me, it’s irrelevant.

67

What do you mean you don’t believe in Bigfoot? I have photographic proof!

68

Ha! I literally just now made this before popping in here and seeing your version.

(That’s of course the Patterson–Gimlin film. And the toys are supposed to be the Loch Ness monster, Mothman, the Abominable Snowman, and an alien.)

69

Found another thing ChatGPT can’t do well yet. Ask it to draw all 5 platonic solids or a full set of modern RPG dice.

70

I just noticed a new ChatGPT feature in the web UI. Over in the sidebar, there’s a “Library” button. In there are all the images I’ve generated so far with this new version of ChatGPT.
I found a few in there I don’t recall seeing before, mostly variants of things I’d done. I think they were ones I thought had failed.

71

I found one last night: creating walking mushrooms that have feet, but not arms. I was trying to create realistic versions of characters from the manga/anime Dungeon Meshi/Delicious in Dungeon and wanted to add a few of them. Despite saying in the prompt that they don’t have arms, and telling ChatGPT to redo it a few times pointing out that they don’t have arms, it always gave them arms. I ended up hand editing the best of the images to get rid of them.

Based on this reference image, using this prompt.

Summary

Create a realistic image of Izutsumi from Dungeon Meshi/Delicious in Dungeon. She is in a wide dungeon corridor with walls made of rugged, ancient stone blocks. The corridor is lit by flaming wooden torches in wall sconces. There are several walking mushrooms running near her. (A walking mushroom looks like a real mushroom with a colorful spotted cap and a thick stalk, but instead of being rooted to the ground it runs around on two stumpy legs that end in downward-facing mushroom caps instead of feet. A walking mushroom has no face and no arms.) Widescreen Kodachrome DSLR image with shallow dof and forced perspective. Frame the image far enough out that Izutsumi is visible from head to toe. Portrait Kodachrome DSLR photo with shallow dof.

Izutsumi resembles the attached image, but make her look like a living person, not a plastic figure. Make sure she has the cat ears, a tail, and the black areas. Except for her face her body is covered by very short fur.

As an aside, here’s a group shot created from a drawing, a technique mentioned earlier in the thread, using this reference image

And this prompt

Summary

Create a realistic image of the team from Dungeon Meshi/Delicious in Dungeon. From left to right are the human knight Laios, the elf Marcille, the halfling Chillchuck, the dwarf Senshi, and the catgirl Izutsumi, which is the order of the characters in the attached reference image. Place them in a very large room with walls made of rugged, ancient stone blocks lit by a flaming wooden torches in wall sconces. There are scary mythological creatures lurking in the background behind them that are slightly out of focus. Widescreen Kodachrome DSLR photo with shallow dof.

72

I’ve had that happen before. It would give an error message (a “something is wrong” message, not a “I’m not allowed to do this” message) and then the image would later show up.

73

I noticed it lost the neko’s fur, color patttern, and the high shoulder-neck guards on the tank’s armor. No doubt a bunch of other character-defining details that a fan of that manga(?) would notice and think “Did the costume designers on the live action version never even bother looking at the original?”
I’ve been running into the same problem. My original characters keep losing this or that feature of their costume or appearance that I consider iconic. It is so close to being able to do consistent characters, but not all the way there yet.

74

On the individual image, every early version of the prompt ended up with the fur as clothes, or when I insisted that it was fur made all regions black, and the first version left her looking much more like the plastic model. Lots of the oddly over-specific descriptions in the final prompt are lessons learned from eariler images.

I started off wanting Alf sneaking up behind her with a large fishing net (because catgirl). I got the plasticy interpretation and some random guy. Had to point out that it was Alf the short, furry alien from 1980s TV and she was more realistic. But then the net started looking bad so I changed it to a fork. But then the catgirl looked too old so I asked for her to be younger. But then it overshot and made her creepily young, like maybe 10 years old in that outfit. Then I decided to drop Alf and go with the walking mushrooms, doing three tries that gave them arms. That image I posted was the 10th version.

75

Why do I seem to perceive Larry Hagman kind of drifting into Larry Linville there?

76

Yeah, it got four of the five right, but couldn’t do dodecahedron even after after asking it to redraw it four times (the other four it got right on the first try.)

ETA: It finally got it right when I just asked it for a photorealistic dodecahedron, but when I asked for all five in one image, it got all except that one right.

I’m amused by all the stuff we’re nitpicking (in a good way). I remember c. 2020 there was an early AI landscape generator that was making some buzz, but even fenced in with those contraints, it couldn’t do simple stuff like: make me a landscape with mountains, river, a forest and a sunset with any degree of reliability. Now, stuff like that is just taken for granted.

77

On a similar note, ChatGPT 4o is the first AI I’ve found to be able to do a reasonable Rubik’s Cube:

78

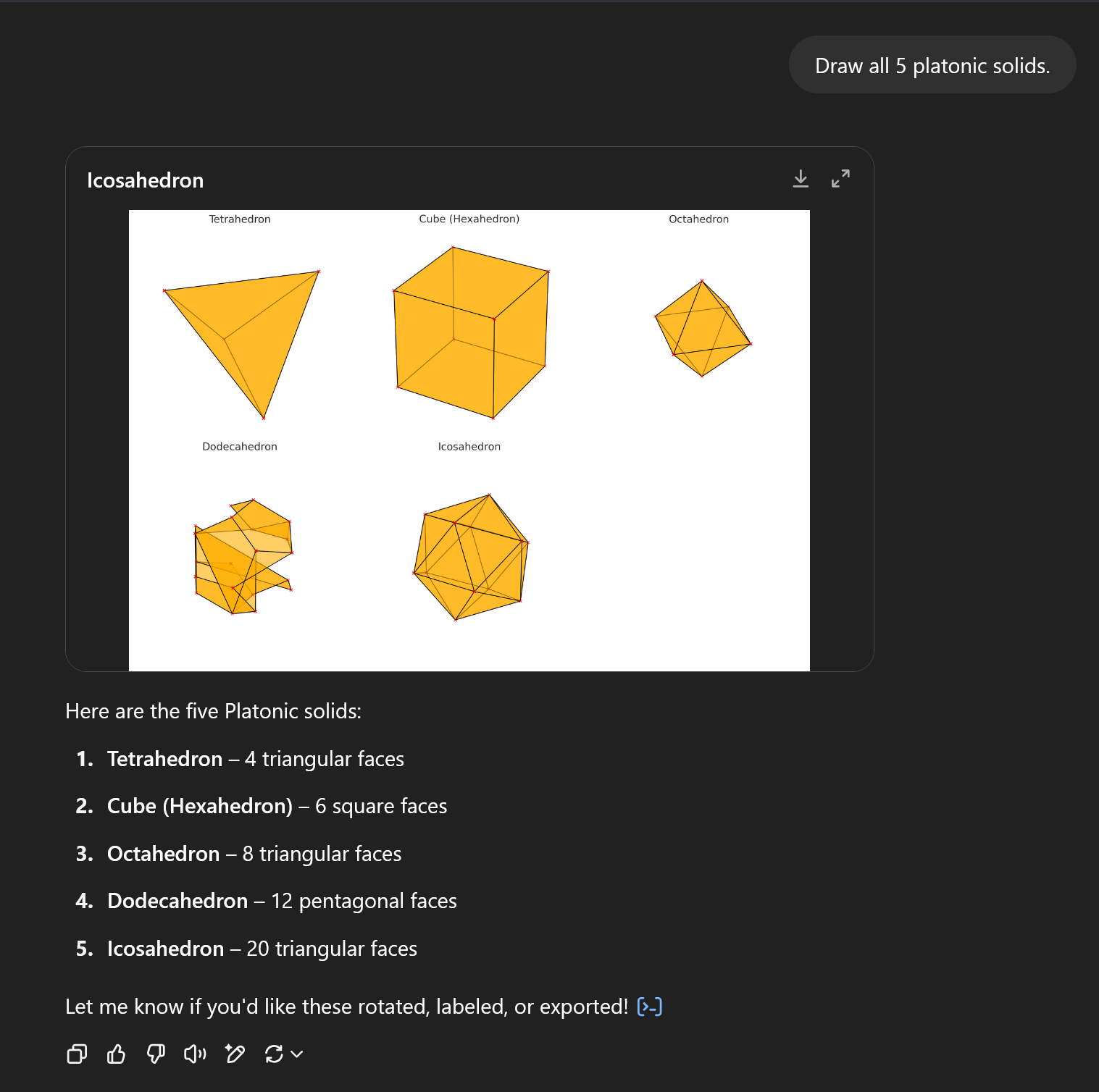
Just went back in and tried an even simpler request for the platonic solids, and instead of calling its new image generator, it decided to try python instead. Still didn’t go well:

For the uber nerdy, here’s the code it generated for that:

Summary 
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import numpy as np

# Helper function to draw a platonic solid
def draw_solid(ax, vertices, faces, title):
    ax.set_title(title)
    ax.add_collection3d(Poly3DCollection([vertices[face] for face in faces], edgecolor='k', alpha=0.6))
    ax.scatter(vertices[:, 0], vertices[:, 1], vertices[:, 2], color='r')
    ax.set_box_aspect([1,1,1])
    ax.axis('off')

fig = plt.figure(figsize=(15, 10))

# Tetrahedron
tetra_vertices = np.array([
    [1, 1, 1], [-1, -1, 1], [-1, 1, -1], [1, -1, -1]
])
tetra_faces = [[0, 1, 2], [0, 1, 3], [0, 2, 3], [1, 2, 3]]

# Cube
cube_vertices = np.array([
    [-1, -1, -1], [1, -1, -1], [1, 1, -1], [-1, 1, -1],
    [-1, -1, 1], [1, -1, 1], [1, 1, 1], [-1, 1, 1]
])
cube_faces = [[0, 1, 2, 3], [4, 5, 6, 7],
              [0, 1, 5, 4], [2, 3, 7, 6],
              [1, 2, 6, 5], [4, 7, 3, 0]]

# Octahedron
oct_vertices = np.array([
    [1, 0, 0], [-1, 0, 0],
    [0, 1, 0], [0, -1, 0],
    [0, 0, 1], [0, 0, -1]
])
oct_faces = [[0, 2, 4], [2, 1, 4], [1, 3, 4], [3, 0, 4],
             [0, 2, 5], [2, 1, 5], [1, 3, 5], [3, 0, 5]]

# Dodecahedron (approximate coordinates)
phi = (1 + np.sqrt(5)) / 2
a, b = 1, 1 / phi
dodeca_vertices = np.array([
    [-a, -a, -a], [-a, -a, a], [-a, a, -a], [-a, a, a],
    [a, -a, -a], [a, -a, a], [a, a, -a], [a, a, a],
    [0, -b, -phi], [0, -b, phi], [0, b, -phi], [0, b, phi],
    [-b, -phi, 0], [-b, phi, 0], [b, -phi, 0], [b, phi, 0],
    [-phi, 0, -b], [phi, 0, -b], [-phi, 0, b], [phi, 0, b]
])
dodeca_faces = [
    [0, 8, 10, 2, 16], [0, 16, 18, 1, 12], [0, 12, 14, 4, 8],
    [1, 18, 6, 10, 8], [1, 8, 4, 5, 9], [1, 9, 11, 3, 13],
    [2, 10, 6, 17, 16], [3, 11, 7, 15, 13], [4, 14, 19, 5, 8],
    [5, 19, 7, 11, 9], [6, 18, 16, 17], [7, 19, 15, 13]
]

# Icosahedron
ico_vertices = np.array([
    [0, 1, phi], [0, -1, phi], [0, 1, -phi], [0, -1, -phi],
    [1, phi, 0], [-1, phi, 0], [1, -phi, 0], [-1, -phi, 0],
    [phi, 0, 1], [-phi, 0, 1], [phi, 0, -1], [-phi, 0, -1]
])
ico_faces = [
    [0, 1, 8], [0, 1, 9], [0, 4, 5], [0, 4, 8], [0, 5, 9],
    [1, 6, 7], [1, 6, 8], [1, 7, 9], [2, 3, 10], [2, 3, 11],
    [2, 4, 5], [2, 4, 10], [2, 5, 11], [3, 6, 7], [3, 6, 10],
    [3, 7, 11], [4, 8, 10], [5, 9, 11], [6, 8, 10], [7, 9, 11]
]

# Plot each solid
ax1 = fig.add_subplot(231, projection='3d')
draw_solid(ax1, tetra_vertices, tetra_faces, "Tetrahedron")

ax2 = fig.add_subplot(232, projection='3d')
draw_solid(ax2, cube_vertices, cube_faces, "Cube (Hexahedron)")

ax3 = fig.add_subplot(233, projection='3d')
draw_solid(ax3, oct_vertices, oct_faces, "Octahedron")

ax4 = fig.add_subplot(234, projection='3d')
draw_solid(ax4, dodeca_vertices, dodeca_faces, "Dodecahedron")

ax5 = fig.add_subplot(235, projection='3d')
draw_solid(ax5, ico_vertices, ico_faces, "Icosahedron")

plt.tight_layout()
plt.show()
79

Ehh, enough messing with the platonic solids for now. This all started when I asked for an image of the “Bit” character from Tron, and got the image in the lower right hand corner.

80

Have you tried doing Tron himself? I once did Robocop and Tron at a outdoor French cafe sharing a strand of spaghetti like Lady and the Tramp. It nailed Robocop, mostly failed Tron.