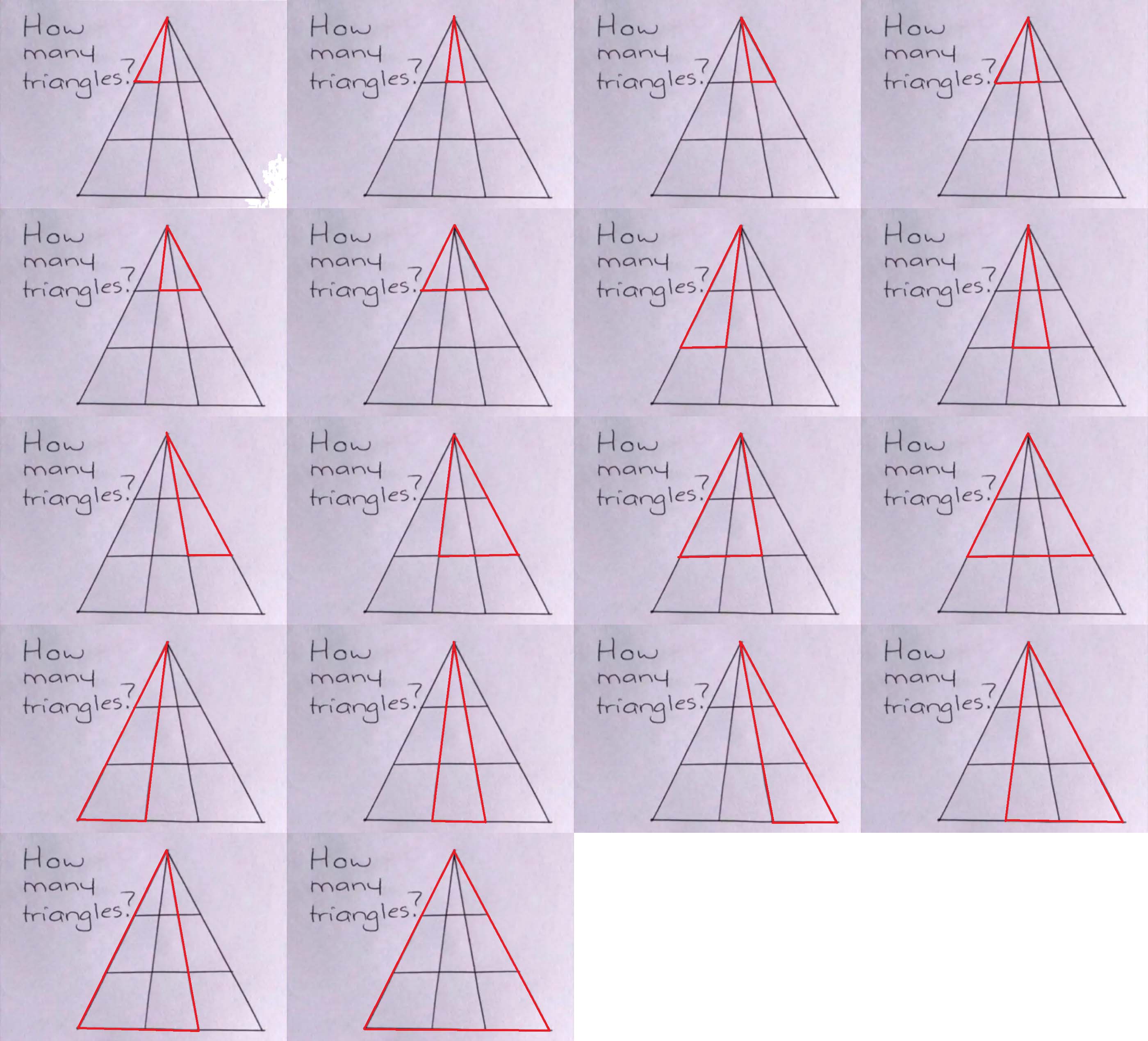
Wait, I double counted those in the center and the overall. 18.
If you label each section of the drawing, 1 2 3 across the top, 4 5 6 across the middle, and 7 8 9 along the bottom, the triangles I count are:
1
2
3
1 2
2 3
1 2 3
1 4
1 4 7
2 5
2 5 8
3 6
3 6 9
1 2 4 5
1 2 4 5 7 8
2 3 5 6
2 3 5 6 8 9
1 2 3 4 5 6
1 2 3 4 5 6 7 8 9
Which is 18.
The answer is 200.
Now guess what base I’m using.
That would be 18 in Base 3, right?
That depends what base you are writing “18” in.
Base 10.
But then what base is the 10 in…?
Agreed. That would not be suitable here for a FQ question. It should have been posted in IMHO.
Well, 4 in a “window” count. 3 triangles to form the window, and the window itself is triangular so add it.
If the rule was “overlapping not allowed” people would still say 4, because of the window exception to the overlapping rule.
Is there a “transparent edges not allowed” rule ? 
I got 26, starting with viewing it as a drawing of a 4 sided pyramid, then shifting my perspective to that of a flat, overlapping bunch of triangles. But I did break the rule about guessing and counted.
There are an infinite number of triangles, that’s my guess. Seems like math puzzles often wind up with infinity somehow, so there.
18
18 is a sacred number in Hebrew (well, in Judaism), because it is the value of the word life-- every word has a numeric value, since letters are reused as digits. I wonder if someone deliberately constructed the triangle so the answer would be 18.
The article linked says the correct answer is 18, but the only rule stated is you must guess, so I disagree, it’s a 3d drawing of a pyramid or a flat drawing of overlapping triangles depending on perspective based on the problem as stated in the article.
Is there another article somewhere that has the rules actually stated that would limit the correct number to 18?
Also, dammit, I try not to get sucked into these ambiguous gotcha/ football moving kind of things.
Each pixel is actually a triangle surrounding another triangle surrounding another triangle until you get down to turtles.
Triangle Man hates Particle Man.
While such a drawing may represent a 3D shape, the drawing itself is 2D. So I would not consider a 3D interpretation valid.
Sure, some people talk about the triangles “overlap,” but that doesn’t mean they’re 3D shapes. It’s just a way to describe how line segments (and portions of line segments) may be reused in other triangles. They still all exist on a 2D plane.
I do understand that there are similar puzzles that only work if you assume the object is 3D, but those tend to ask you to count an object that could be assumed to be 3D. If you asked how many triangles are in a pyramid, a valid answer would be “an infinite number,” as there are an infinite number of triangular cross-sections.
Which leads immediately to puzzles like: How many squares in this picture?
When you’ve figured that out, try these (again, how many squares?):
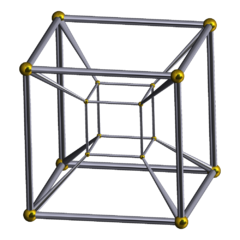
The first one is 24 squares (and 32 edges), assuming it’s meant as a representation of a 4-d hypercube. The second one is 80 squares, assuming it’s meant as a representation of 5-d.
The third one appears to be merely 3-dimensional, with an easily-counted 36 squares, unless I’m missing something.
Entirely too many.
There’s plenty more where those came from. 6-d cubes next? Then 7-d?
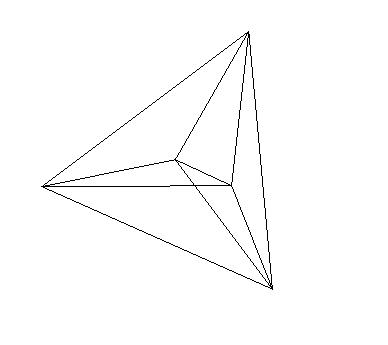
Oh, wait. This thread is about triangles! Okay, how many triangles here?
It’s a 4-d “tetrahedron”. Like cubes, these can also exist in any number of dimensions. Apparently the term for an arbitrarily-high-dimension “tetrahedron” is a n-simplex. How many triangles in a 5-simplex? A 6-simplex?
There’s a pattern to these that’s very straightforward and many readers of this Board are probably very familiar with it, even if you don’t know it!