The part that’s surprising to me is that that bending is, ultimately, being enforced by the rails that the train is running on. So two rails are forcing the bending of 50 rails. Granted, those two rails are pretty firmly attached and reinforced to the ground, but still.
It seems that welded-rail trains in the US have been known to go around curves of 360-ft radius.
Probably only takes a few thousand pounds of pull to keep a load of quarter-mile rails moving at 20 mph on straight, level track. So when it enters a sharp curve that’s longer than the train, how much does the required pull increase?
Next question: would greasing the curve be a bad idea.
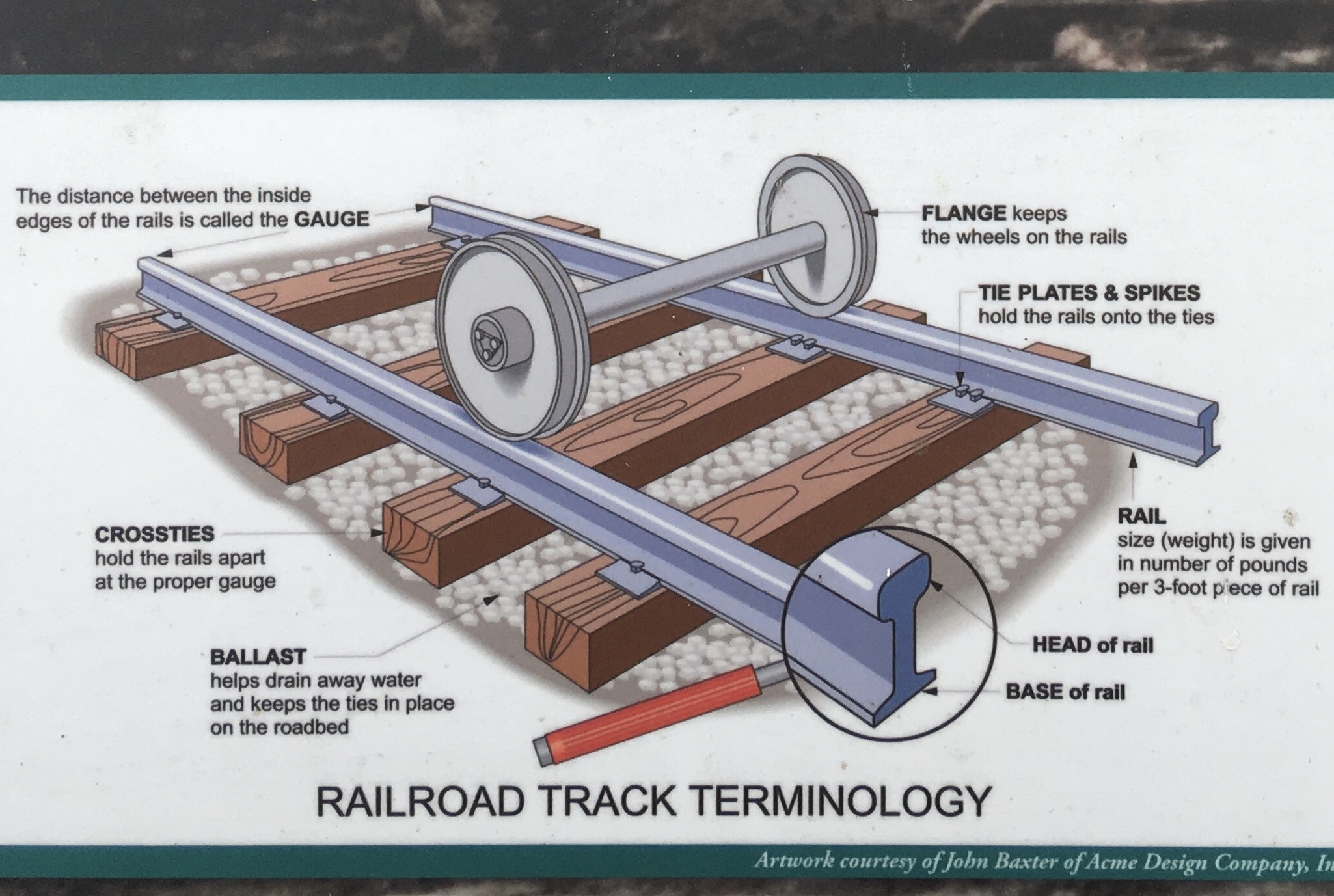
The rails that the train runs on are attached to crossties by tie plates and spikes which controls the gauge (parallel distance between rails), and the ties are loosely embedded in the track ballast (loose aggregate), but what really holds the track down is the weight of the train and its load.
The rails themselves are really just bearing local shear and compressive loads; all of the resistance to the longitudinal flexure of the rails being transported is borne by the roadbed, which again is compressed by the load being carried. Track rail is typically AISI 1080 Q&T with a tensile strength of 130–160 ksi (900–1100 MPa), which would give a limiting shear strength of about 70–90 ksi (about 480–620 MPa), so for ASCE 60 lb rail (the lightest common type) with a web thickness of 31/64 inch it can resist up to 400–520 kilopounds per linear foot (or 5.8–7.6 x106 N/m if I’ve done unit conversions correctly).
Trains and rail systems use on-board and wayside greasing mechanisms to apply lubrication to reduce frictional losses and wear.
I have only briefly worked on train systems (and never on actual track layout), and I know that at least we used to have a couple of posters who actually worked in the rail industry so I welcome any corrections, but in essence the roadbed (under the weight of the load being carried) is doing all of the ‘work’ to keep the train turning as intended, and if you cut the rail sections in between bogies it would have no affect, at least until the wheels encountered a gap int he rail at which time they would definitely derail with the outcome as seen in the o.p.
Stranger
I did a bit of math. How much energy did it take to bend those rails? The formula for the energy in a bent, slender beam is:
U=\frac{EIL}{2R^2}
Where:
E = Young’s modulus for steel = 2e11 N/m^2
I = Second moment of area for a rail = 6.4e-6 m^4 (estimated by approximating the cross-section of a standard rail with two rectangles)
R = radius of curve = 125 m (guesswork)
L = length of track = 0.125*2*\pi*125 m (assume a 45 degree curve) = 100 m
So we get U=4100 J. There are 50 rails, so really 205 kJ. Not much at all. Only a few dozen horsepower required to perform that over the course of several seconds. And once bent, there’s no additional energy required.
Plus …
Once the leading edge of the cargo rails are out of the curve onto the straightaway, they’re un-springing back to straight. And so giving up (most of) the energy that went into bending them. Whether any of that energy is usefully recovered into moving the train or it’s all just heat I can’t say. But it’s going somewhere.
Unless you’re deforming the rails past their elastic limit, in which case you’d also need to spend energy to straighten them again. But they probably ensure there aren’t any turns sharp enough for that to happen.
Right–that’s what I meant by not needing additional energy. The unspringing should recover most of the energy that went into it, and this is a continuous process as the bent part travels down the train. There will be some losses due to friction but I’ll bet it’s >80% efficient (I’d guess there are wheels or at least lubricated slides allowing the rail to move). And when the train as a whole leaves the curve, it actually gets a boost.
I don’t see the mechanism for that. Considerable energy is expended in bending the rails going around the curve, and the locomotive has to pull harder. But when the train returns to straight track, and the rails straighten out, I don’t see how that can provide any propulsive energy to the train, or at least none of any significance.
The analogy I would draw is pulling a stiff, springy wire through a pipe with a small curved section. While the wire is being pulled through the curve, it has to be pulled harder in order to force it to bend. But when the wire clears the curve and straightens out, that extra energy isn’t recovered – it’s just lost to heat.
The entire system is reversible. If it takes energy to send the train into the curve (and it does, clearly, since the rail stores energy), then it recovers energy coming out. If you sent the train partway into the curve and disconnected the engine, it would be pushed out backwards.
Of course there’s some friction in the system, so it isn’t perfectly efficient. But trains are pretty good in that regard.
Not true. The end of the springy wire will be squirted out as it leaves. I’ve seen this effect many times. It does however require the inside of the pipe to be low friction, and the wire to be actually springy.
The mechanism is that the back end of the wire, in trying to straighten out, is pushing against the side of the barrier, but the front end of the wire, that’s already in the straight section, isn’t pushing against anything.
OK, thanks, I think I kinda see that now. But … wouldn’t that depend on how far into the curve you were before you disconnected the engine? If only the first few cars were into the curve, I can see how releasing them would push the rest of them backwards. But if only the last few were still in the curve, it would surely push the rest of them forwards. And if the loco was uncoupled when the set of cars was exactly halfway around the curve, they wouldn’t go anywhere at all, because now you have a symmetrical configuration with no directional preference.
So I’m not seeing how this amounts to efficient energy recovery, except when the last few cars come out of the curve and give the train a bit of a push, because in different phases of the configuration the cars are either resisting the pull, neutral, or, finally, pushing forward.
Yes, that’s right. When there are cars ahead of and behind the curve, it’s symmetrical and neutral, as you noted. So it takes no extra power to move the train in this state. But the initial energy investment as the train enters the curve is recovered as it leaves. And as stated above, it’s not much energy. I doubt the train engineer has to think about it at all. The train would slow by a tiny fraction of a mph as it enters the curve, and get that tiny fraction back as it leaves.
Not to belabor this technicality to death, but I would suggest that the effect of frictional losses is being grossly underestimated here, and that the forward impulse that the train gets as the last of the cars come out of the curve is a negligible fraction of the original energy input due to all the friction, noise, and vibration as the rails rub against their restraints, because this is so very far removed from a theoretical perfect spring. And as you point out, the energy stored and released is very small relative to the momentum of the train and the potential loss factors.
So my initial objection was answered, and I see how the dynamics of energy recovery could work in theory, but I’m going to counter your guesstimate – on this tangential question that probably doesn’t have a good hard answer – that in practice the amount of recovered energy is probably closer to zero than 80%.
That the energy recovery is likely lost in the noise doesn’t mean it’s close to 0%. The rail itself will have almost perfect recovery. I suspect the losses from the rail sliding against the constraints is also small, since it’ll be slow and they probably grease it up to prevent damage. The train itself has some friction but that was true anyway and the spring effect isn’t going to significantly alter that.
So the whole thing is analagous to a train cresting a hill. At first the engine is dragging the front of the train up the hill. Eventually the engine crests the hill & some cars are still climbing while others are descending. Later the last car crests and the wholevtrsin is downhill or onto the subsequent flats.
There are frictional losses throughout. But the big picture is powerplant energy converted to first kinetic energy then gravitational potential energy then back into kinetic.
Close, but a significant difference is that there is only one neutral point when cresting a hill (when there’s equal weight on both sides), whereas with the curve it’s neutral for the entire range except for where the rail is partially through the curve. So it’s like cresting a hill with a long flat spot on top (longer than the train). But yeah, overall a pretty good analogy. And the basic physics is the same even if the “hill” is only 3 inches tall and you can’t actually notice the effect.
Thanks for the refinement. Yeah, hills are generally longer than trains whereas curves are generally shorter than modern prewelded ~1300 foot rail sections.
There are exceptions in both directions of course.
Bending rail manually is a PITA. I belong to a museum where track maintenance is done by volunteers. Most of our rail is in 60 to 80 foot lengths. When we need to bend one for a curve there a clamp rig similar to a “come along” or chain fall. Move the rig 18 inches or so at a time along the full length applying X amount of manual leverage. Rail bends a hair. When you reach the end, you know how well you did. With experience the “old guys” can usually get the correct amount of bend or curve in no more than two passes. But it’s hard, hard, hard work.
Although it’s called “destressing”, I’ve always thought that “re-stressing” would be a less confusing term, since the aim is to put the (welded) rail in even tension.
In use, the system requires occasional maintenance. The rail bed has to be repaired, rails and junctions cut and replaced. By default, this has the effect of releasing the tension in the area of the repair (unless you do it on a /very/ hot day). The development of longer and longer welded sections has gone hand-in-hand with the development of repair methods to re-tension the repaired sections, but eventually/traditionally, you have to unfasten a whole rail, end-to-end, and re-tension it.