But that’s not really a “plotter” is it?
More of an electronic spirograph.
Also, the “tap” you impart will be digitized, so the number of unique curves will still be limited by the resolution of your D/A.
Thanks to all for helping to fight my ignorance. My main exposure to 3D curved surfaces is video games, where the video card has to use tricks like anti-aliasing to smooth out the jaggy polygons.
Anti-aliasing is not a method to smooth out surfaces that are subdivided and rendered as a polygonal faces. To put it simply, if you draw a white line on a black background, you would get a jaggy appearance due to the fact that the line is approximated by pixels. Instead you can draw certain pixels adjacent to the line with various grey levels to make it appear smoother.
Hm. I apologize if this is actually what you meant, it just seemes a bit unclear from your post.
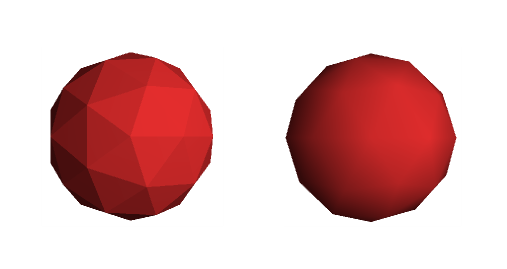
To make polygonal surfaces seem smoother you can use smooth shading techniques where the flat faces are made to appear smooth by varying the lighting over the faces. This is implemented by not using the actual rendered polygons’ normals in the lighting calculation, but instead interpolating the normals between adjacent faces. In the same vein, bumpmapping retrieves the surface normals from a texture to make a flat surface appear more detailed than it is.
Here’s how the interpolation of normals makes a polygonal sphere appear smoother:
Pixar’s films do not use raytracing, they use RenderMan, which uses the REYES algorithm. RenderMan does allow for shaders to implement limited raytracing, so Pixar artists can place raytracing shaders on important items in the scene when necessary. You might be thinking of Blue Moon, a RenderMan-compliant raytracer.
Raytracing is not easily parallelizable because a ray reflected off of a given surface can theoretically hit any other object in the scene, so caching performance is poor without some very complex algorithms.
A vector display doesn’t only draw with straight lines. You do know that the digital signal from the computer can be turned into a smooth analog one, right? Filtering the D/A output gives you a smooth signal, not a set of straight lines. A plotter could conceivably work the same way, as psychonaut described.
For some values of “smooth.”
The bottom line is: all paths are being drawn with line segments, not continuous curves.
Neither of these devices have the infinite resolution requested in the OP, although they may satisfy his real-world requirements.
Please explain why you think a sine wave isn’t a smooth curve. Or why the output of a DAC can’t be filtered to one. At least down to the granularity of the fundamental physics involved, which didn’t seem to be what you were implying, as you seemed to be saying it was inherent in being a digital computer.
Are we talking about rendering a curve (in pixels or on a plotter etc) or calculating a curve? I’m sure that teh calkulus can give some pretty good curve data. If the former. . . finer grained resolution in whatever output medium, no?
Basically, computers can represent curved surfaces directly, easily, as has already been mentioned (and then render them to your pixellated screen the same way as anything else). But specializing to do just one thing and do it really well makes everything faster, especially when that specialization is done in hardware. One simple thing you’ll want to do often is render triangles, the simplest surface in some sense. So, you have specialized hardware for doing lots of triangle rendering, and you have programs that try and turn everything into rendering triangles (even the polygons you’re referring to are generally not one atomic unit, but rather a bunch of coplanar triangles). Things could be different, but the more heterogenous and idiosyncratic what you do is, the harder it is to optimize and the less likely someone will give you a card that’s specially crafted to your particular purposes. Do one thing, and do it well; that’s the way to get breakneck speed.
This might be getting a bit technical.
Remember, we are talking about moving a pen across paper. Generally, this is done by attaching the pen to a leadscrew, which changes rotary motion to linear motion. It can also be done with gears and a belt. The screw is driven by a motor. Most of these motors are steppers - they only move in discrete steps, creating a lower limit on the smallest incremental pen move. I suppose it’s possible that you could replace them with servos, which are theoretically capable of smooth motion, but even in this case, the feedback from the servo is generally a digital encoder, once again limiting your minimum increment.
But, let’s say you have some system with infinite resolution. Now, you still need to drive it from a digital system, which means a D/A at some point. You can filter the D/A to smooth the steps - BUT - the filtering only works correctly for certain frequencies. Think of it this way - say you had some very low frequency steps, corresponding to a very shallow curve. You would need to have a huge low-pass filter to smooth those steps out, which would then completely mess up any fine motion.
So, for very specific circumstances, you could probably draw some very nice smooth curves, but the general case is always going to have measurable steps.
Note that all of this is academic, since the resolution of the stepper motors is smaller than the width of the pen (although you can still see the steps on very shallow curves).
A vector display has many of the same issues, but also has the same solution - the spot size is always bigger than the minimum step. Note that vector displays have all kinds of other issues, which is why they fell out of favor (redraw time increases with the number of vectors, they require very fast blanking amplifiers, and they require careful tuning to prevent overshoot).
I don’t think the OP’s beef was with the pixels when he mentioned “polygons” or “little flat shapes”, as he also mentioned that his main exposure was curved surfaces in games. Of course, taking the issue a step further you arrive at the problem you’re discussing now. But I guess it’s common here to follow questions to their academical conclusions :). Carry on.
beowulff, I wasn’t talking about plotters at all. I was specifically criticizing your assertion that a vector display can’t draw a smooth curve. They aren’t driven by stepper motors or anything similar, so none of those arguments apply. In a practical sense, it’s pretty hard to get them to draw something that isn’t smooth (a polygon will have rounded edges). With a CRT it is in some sense impossible at higher frequencies (because the deflection fields can’t change quickly enough).
A filter removing the ability to do ‘fine motion’ as you call it has nothing to do with whether it can output a smooth curve. Even to draw merely line segments necessarily requires filtering from an ideal DAC. Otherwise it’d be nothing more than a collection of dots on the screen.
Once again, it depends on your definition of “smooth.”
For the vast majority of people, even a raster display is “smooth.”
Neither is “smooth” at a microscopic level.
I’m using smooth roughly in a mathematical sense - at the very least continuously differentiable.
I fully accept that at a small enough level, so far as we can observe, everything is more or less discrete.
In your opinion, does an analog signal source have the same issues that a “digitally derived” signal would? Because what you’ve said so far in this thread suggests that you would say no, and that’s unrelated to the fundamental physical limits (assuming that’s what you meant by ‘microscopic’.)
Henrichek, I think you did give the best answer to the OP, which seems to be more about graphics processing than display per se. We could also have discussed whether particles/voxels will ever make a comeback. That wouldn’t be ‘efficient’, but it’d help with some of the physics problems.
Mathematically, curves are always smooth…
In the real world, even generating a pure sine wave is impossible - there are always distortions. As an engineer, I need to focus on what is achievable in the physical world.
So, if I want to display my mathematical model, I need to understand the the display is just an approximation, albeit possibly a very faithful one.
Those are nice generalities, but really don’t speak to your claim that a vector display only draws using straight lines. Such things are impossible in the real world, too, so why would you even claim that much if such was your original position? Even psychonaut had already mentioned physical limitations.
I didn’t mean to imply that a vector display could only draw straight lines, it’s obvious that you can cause the electron beam to move in “smooth” curves - however, if the beam was infinitely thin, and you overlaid your mathematical curve on top of the beam trace, you would see that they don’t match - so, you can filter your output to smooth the curves, or you can have stair-steps, and more faithful rendering of rapid changes.
I’m not sure what the OP was looking for - he was talking about “drawing”, which is where the plotter came up. It’s pretty clear to me that current computer technology has no problems drawing curves, at least well enough to satisfy most users.
My guess is simply that he has observed curved surfaces as being rendered by tesselating them into smaller triangles. I also think he didn’t go even as far as challenging the display pixels. At least that was the basis of my answers. Maybe I’m wrong.
That doesn’t detract from an interesting theoretical discussion though.
I think Henrichek is absolutely correct. The OP is clearly talking about 3d games using noticeably using polygons (and really, just triangles) to render most surfaces.
So why did you say, “Both only draw with straight lines.”? Either the curve drawn is smooth or it isn’t, and if it’s made up of straight line segments, it’s not smooth (in the sense I’ve established I’m using, which perhaps I should have clarified before).
To rephrase an earlier question: If the input to the display is an ideal pure sine wave, would you say the curve that results is only drawn with straight lines?