Like I’ve been saying, there’s not much difference in the ludicrous-speed treadmill scenario and a scenario in which the plane has tires that are completely flat and a set of cracked bearings (in other words, not so much wheels as poorly-formed skids). Same forces at work, just more dramatic in the latter example.
Oh for God’s sake. If you don’t understand something, just ask. Don’t go off all in a huff.
Take a look at your own drawing, right here. Add a force on the bottom of the wheel pointing to the left. Now the forces on the wheel are unbalanced, and one of two things must happen. Either the force is balanced by an opposing force to the right, leaving the body in equilibrium, or the wheel accelerates to the left (F=ma). Or a combination of the two, of course.
If the former, the only other place a force can be transmitted is through the bearing. You do understand that forces in general can be transmitted through bearings, right? The weight of the plane for instance? I ask because you seem pretty adamant that forces can’t be transmitted, and I’m sort of at a loss to understand why you might think that, since transmission of forces is essentially what bearings do.
And while I’m at it, have you worked with free body diagrams before? Static equilibrium? F=ma? Again, I ask because you seem not to believe things that are self-evident to me. It’s difficult to gauge an explanation without knowing one’s audience.
This is not true and I think it is the crux of understanding the problem. If the engine is producing thrust and the treadmill is at a constant speed the plane will move to the left. It is only by accelerating that the treadmill can counter the thrust, and the state of equilibrium will occur at a constant acceleration of the treadmill, not a constant speed.
That’s the piece that isn’t correct that treis is commenting on. The “answer” here depends on your assumptions, but if the treadmill imparts any horizontal force on the tire, most or all of the force is transmitted to the plane through the hub. Friction is there too, yes (if friction is part of your original assumptions), in the bearing. But the horizontal force has to “go” somewhere, and that somewhere is into the plane.
Again depending on assumptions, but everything you say here I’d agree with.
My mistake, I missed the bit about the mark on the ground. You’re correct - the question as described defines a stationary condition for the plane. What has to physically happen to maintain that stationary condition is another matter!
I still contend that in your example, the wheel can be accelerated to roll forward along the belt without slipping, and that the marks on the wheel and belt will continue to line up as the wheel progresses along the belt. However, the circumferential speed of the wheel relative to its centre of rotation will be higher than the speed of the belt, so the OP’s conditions as you are interpreting them are not met.
The circumferential speed of the wheel relative to the ground, at its point of contact with the belt, will always match the speed of the belt, whether the wheel is progressing along the belt or not. This confused me for a bit, before I realised that it isn’t relevant to the problem. The point of contact of a wheel rolling along a surface has an instantanous velocity of zero relative to that surface.
All right, then. Apropos of a number of posts in this thread (no single post, but the cumulation of multiple posts), let’s talk about forces and force transfer. Let’s talk about forces in the context of, say, a wheel:
*******
** **
** **
* *
* *
* *
* O *
* *
* *
* *
** **
** **
*******
The wheel is round, and it has some mass, m, with a center of mass in the center of the wheel at “O”. It’s also got rotational inertia, I. One way to think of mass is as the resistance of the wheel to motion when a force is applied. In the same way, rotational inertia can be thought of as the resistance of the wheel to rotation when a torque is applied. With me so far?
In addition, let’s assume that the wheel has a bearing in the center, at the “O”. The other side of the bearing is connected to Something. We haven’t defined what Something is, yet, but we will. Be patient. Let’s make this simple and assume the bearing is frictionless. We can add friction in later if we want, but let’s keep it simple for now. Now, the bearing is a pin joint–it allows both horizontal and vertical forces between the wheel and the Something that it’s connected to, but does not allow torques to be transferred.
One last thing. Let’s make this wheel and the associated forces as simple as possible. So let’s ignore gravity and everything else. No gravity, no treadmill, no Earth, no nothing. This is, right now, just a wheel in space connected to Something through the bearing. OK. Got it?
Now let’s change the story.
*******
** **
** **
* *
* *
* *
* O *<----F
* *
* *
* *
** **
** **
*******
I’ve added a force F on the wheel; this force F passes through the center of mass. This force is, as drawn, unbalanced, and it isn’t yet the whole story. From here on out, a few different things could happen.
Suppose the wheel isn’t connected to anything at the bearing (the Something is Nothing, in other words). In this case, there’s no way the force F can be resisted, and the entire wheel will accelerate to the left. The acceleration, in fact, will obey Newton’s law, F = ma.
OK, but what if the wheel is actually connected to Something? What if that Something was the ground, and the wheel is prevented from actually moving to the left? In that case, there will be a reaction force at the bearing. The wheel will push on the ground, through the bearing, and the ground will push back:
*******
** **
** **
* *
* *
* *
* R---->O *<----F
* *
* *
* *
** **
** **
*******
The ground will push back, in fact, so that R exactly equals F. This is the key: because the wheel does not move, the forces must be add to zero. If they didn’t add to zero, the wheel would accelerate to the left or right. But it doesn’t. So the forces must be balanced, and the force F is transmitted to the ground.
Another possible thing that could happen would be that the Something that the wheel is connected to is something very massive, but moveable, which has a mass M. In that case, as soon as the force F is applied, everything accelerates–both the wheel and the Something–at an acceleration of F = (M+m)a. In this case, there will still be a reaction R on the bearing, but the reaction R will be less than F. How much less is left as an exercise to the reader.
All right, got all that? Now let’s do something a little different. Let’s move the force:
*******
** **
** **
* *
* *
* *
* O *
* *
* *
* *
** **
** **
*******<----F
Now the force F is no longer a the center of mass. How does that change things?
First or all, let’s go back to the assumption that the wheel is just free in space–nothing is connected to the bearing. In this case, the wheel will still accelerate to the left in accordance with F = Ma. The force F is still unbalanced, and the unbalanced force must result in an acceleration. However, the wheel will also rotationally accelerate. The force F is not through the center of mass, and that creates a torque T = Fr. This torque rotationally accelerates the wheel through the rotational equivalent of Newton’s law: T = I[symbol]a[/symbol] ([symbol]a[/symbol] being rotational acceleration). So the wheel will begin to move to the left, and spin clockwise.
Now let’s assume, instead, that the wheel is connected to the ground at the bearing–the Something is the ground again. This gives a case like so:
*******
** **
** **
* *
* *
* *
* R---->O *
* *
* *
* *
** **
** **
*******<----F
Here’s the key question: does the center of mass of the wheel accelerate to the left? No! it’s connected to the ground! It can’t move to the left. And because it can’t move to the left, the forces must add to zero, and the force R equals the force F.
Of course, the difference between this case and the one above where the force F was pointed toward the center of mass is that now the wheel will spin. And we can calculate exactly how much it will spin: the two forces set up a torque T = Fr, which rotationally accelerates the wheel through the rotational equivalent of Newton’s law: T = I[symbol]a[/symbol].
So all that leads to the real question: how does this apply to an airplane? The point is, to keep an airplane from moving, you need to apply a force F to the plane that is equal and opposite the engine thrust. Assuming the plane won’t flip end-for-end or anything silly like that (adding back gravity and so forth), it doesn’t matter if that force is applied to the nose of the airplane, or the tail, or the landing gear.
It doesn’t even matter if the force is applied at the bottom of the tires. That force will still be transmitted to the plane and oppose the engine force. Given that this is a thought experiment, it is possible to apply an opposing force to keep the plane in place via the tires. However, this will come at the cost of rotationally accelerating the wheels. And that acceleration is apt to be very large.
Good post zut
I agree that ZUT’s post was a good one. What I’ve been trying to understand is why
so many people couldn’t grasp the idea that the OP was a hypothetical question and
all this stuff about mechanical restrictions and “magical” properties was totally
irrelevant. If it were a discussion about the speed of light and time I think most would
understand that it was strictly hypothetical, but here many were trying to dismiss the
problem based on real life probabilities.
zut, in the last diagram, will r=f?
Or will 0<r<f because some of “f” is used to rotate the wheel?
r will equal f if there is no linear accleration. No “f” is “used” to rotate the wheel. The linear acceleration and rotational acceleration are independent of each other.
In the last diagram, R=F because the wheel center of mass does not move. To put it straightforwardly: If a body does not accelerate in a particular direction, the forces in that direction must add to zero.
I think that’s probably the key misunderstanding: there’s an (untrue) assumption that the force F “goes into” spinning the wheel, and is not transferred to the hub. That assumption is, unfortunately, sorta based on physical intuition: push a wheel and it spins, right? However, the spinning is just a “stronger” (i.e., more obvious) reaction to the push. It’s still true that any force must produce an effect: either an acceleration or a reaction force.
(Not a necessary argument, but an additional explanation: You might sense that the offset force F is somehow “different” than the centered force F, because the former produces translational and rotational acceleration, while the latter produces only translational acceleration. Well, you’re right from an energy point of view. It takes more energy to produce both translational and rotational motion. Energy is also proportional to force*distance. In the offset case, the force will “move” farther as the wheel both translates and rotates, delivering more energy. As I said, not a necessary argument, so if this is more confusing than enlightening, feel free to disregard.)
This paragraph captures what I was thinking.
It seems that a wheel that only translates, will translate farther (further?) than a wheel that translates and rotates assuming the same force applied in both cases.
If that is correct, then it seems like the force required to counteract the translation only is less than the force required to counteract the translation and the rotation.
I can see you’ve made a distinction between force and energy, but I don’t understand what I am missing when considering force alone.
Here is a concrete example, but with a bunch of bogus numbers because it’s been a long time since physics and I can’t remember the formulas:
Force=10kgm/s2
Mass of tire=10kg
Radius=1m
Total acceleration=1m/s2
Translational acceleration=Xm/s2 where X<1
Rotational acceleration=R (don’t know units, or how to calc)
Is it true that X+R (assuming conversion to same units, etc)=Total acceleration?
If so, wouldn’t the force to counteract the translational acceleration=MX (not M(X+R))?
No, assuming we have two tires in space. In the first one you apply a force F at the center of mass. There is an unbalanced force F so the tire accelerates linearlly at a rate of F/M. In the second case you apply a force F at the bottom of the wheel. There is an unbalanced force F so the tire accelerates linearlly at a rate F/M. There is absolutely no difference in the linear motion of these two tires. The only difference between them is that in the second case the tire will rotate.
Are you sure you have seperated force and energy? If you are providing the power to move the tires in the two cases above by pedalling on a stationary bike you will have to peddle harder in the second case even though you are providing the same force.
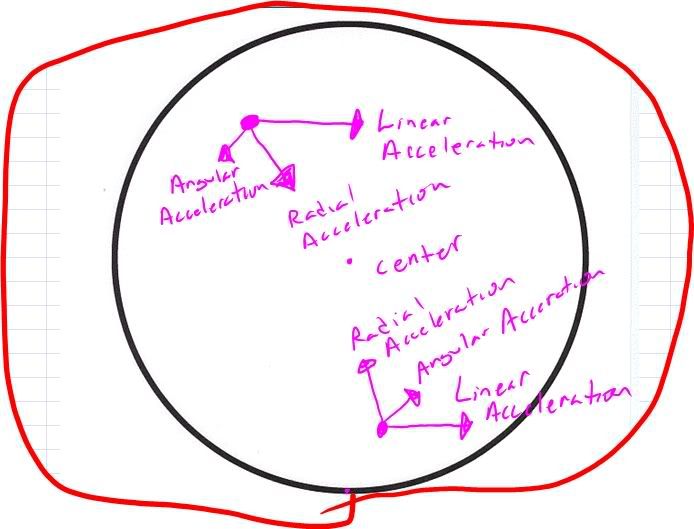
Sort of, for each point the acceleration will be the sum of its linear acceleration and its rotational acceleration. There are 3 components of acceleration in this case, the linear acceleration from the unbalanced force, the radial acceleration which keeps each point on the drum rotating around the center and the angular acceleration that speeds up a given points rotation around the center of the drum. You can add these accelerations up and get the total acceleration for a given point on the drum. But since the accelerations from rotation are different, as you hopefully can see on my picture, at each point on the drum this value will change.
No becuase the R components of acceleration just keep the points on the drum rotating around the center and speed up its rotation. These are independent of the linear acceleration.
Again, don’t get caught up in thinking about the rotation/translation and forget the main point: No acceleration means that the forces add to zero. F = ma. Zero a = zero F.
OK, that being said…
It is a bit confusing that the same force can have different effects. Maybe this will help. Imagine a pair of wheels with an inner hub. The hub is connected to the ground via a bearing–imagine an upside-down caster. There IS gravity. Now: attach a weight W to the two wheels. The left wheel has a weight attached close to the hub, the right wheel has a weight attached far from the hub:
******* ******* g
** ** ** **
** ** ** **
* * * *
* * * *
* * * *
* O W * * O W*
* ^ * * ^ *
* | * * | *
* * * *
** ** ** **
** ** ** **
******* *******
Will there be any diference in the motion between the two wheels? Of course there will! The right wheel will rotate faster. But it’s the same weight, the same force, correct?
The difference is that the right weight travels farther and adds more energy to the system. Same force, different results.
You can’t add translational and rotational accelerations together like that (you can add accelerations, yes, but it’s more complex than that).
I’m assuming in your example you have just the applied force F (no reaction R). In this case, there is a translational acceleration moving the wheel to the left. This is because there is an unbalanced force, F, on the wheel. The acceleration follows Newton’s law, F = ma, or a = F/m. So the wheel moves to the left at 10/10 = 1m/s2.
In addition to the translational acceleration, there is a rotational acceleration. This is because there is an unbalanced torque on the system. The torque is T = Fr = 10*1 = 10Nm. The rotational accelerataion follows Newton’s law T = I[symbol]a[/symbol], or [symbol]a[/symbol] = T/I. You don’t specify the moment of inertia, I, but let’s say it is 10kgm2/s2. Then the rotational acceleration is = 10/10 = 1 rad/s2.
Both accelerations are present, and the force does more work on (delivers more energy to) the wheel than it would if it were positioned throuh the center of mass (and thus causing no rotation).
David Simmons:
Here’s maybe a simpler way to look at it.
First, assume you have some wheels of zero mass sitting on the treadmill, connected to frictionless bearings. If you accelerate the treadmill, there is no force on the treadmill from the wheels, and nothing to resist its acceleration. In this scenario, you’re right. There’s nothing the treadmill can do to keep the airplane from moving. If you add bearing friction, now you’ve got a constant force from a constant treadmill speed. So far so good. This is the point where you and I both agreed (before I had read the more complex scenario Treis put forward).
Now imagine you replace the massless wheels with big heavy ones. At a constant speed, they exert no force on the treadmill, because they’re just spinning around on their frictionless bearings. But if the treadmill accelerates, the heavy wheels will resist the acceleration because of their mass. This couples the axle the wheels are spinning on to the treadmill. If they resist spinning, then the force pulling on them is transmitted to the axle, which is now being accererated in the direction of the treadmill. Once the wheels get up to the new speed, the force stops. But any time there is acceleration from the treadmill, the mass of the wheels couples the airplane to the treadmill to some degree.
So, to keep the airplane from taking off, you need a constant acceleration from the treadmill, so that there’s a constant force on the axle opposing thrust. The more thrust that is applied, the more acceleration is needed to keep the airplane from moving.
This is a ridiculous scenario for the real world, because a constantly-accelerating treadmill would soon be going at insane speeds. But as a thought experiment, it does work. It should be actually pretty easy to test. If you have something like a dumbell kicking around, put it on a towel or something, and put a broomstick in front of the bar of the dumbell to hold it in place. Have someone pull on the towel with a constant speed, and all you’ll feel is the frictional forces once the towel is moving smoothly at the same linear rate.
Now pull the towel with an increasing force so it’s acceclerating. You should feel the different through the broomstick as the dumbell wants to travel with the towel rather than rotate its heavy weghted discs.
At the risk of being dense on this one, if the same force results in 2 different amounts of energy, it seems like we just gained energy.
If the same force is applied, but to different locations of the wheel, and in both cases we get the same translational acceleration, but in one case we get extra rotational acceleration, it seems like we have gained energy.
I would think that the translational acceleration would be considerably less in the case of the force applied at the edge of the wheel.
I know there are other factors in the example I am about to give but, when I play softball, I can think of a similar situation:
- Direct straight on connection of bat and ball causes ball (in my case) to just clear the infield.
- An almost miss that skims the edge of the ball causes the ball to spin significantly and travel in a small arc landing at the pitchers feet.
The issue here is that force and energy are not equivalent. Stand up, walk to the nearest wall, and push on it as hard as you can. You might be exerting a large force, but you are not adding any energy to the wall. That’s because energy is equal to a force multiplied by a distance. When you push on the wall, the distance you push it is zero. Zero distance, zero energy.
Yet you can also push, say, a kid’s red wagon with the same force, and you will add enegy to the wagon. As a matter of fact, you can add different amounts of energy to the wagon.
Thought experiment: Imagine two wagons on the floor. Stand behind one of them and push it as hard as you can, but let go after the wagon has traveled one inch. Push the other wagon not-so-hard, but don’t let go until it’s halfway across the room. Which wagon has more energy?
In addition to zut’s explanation there is also rotational work. As you apply a torque through an angle you transfer energy in the body. Lets say for the first case of the tire (no rotation) a given force at some instant velocity happens. In order for that to happen you need to have an engine putting out a power eqaul to the instantanious velocity time the given force. Now, for the second case (with rotation) power is necessary for the rotation. At a given instant it has a rotational velocity w and a torque T. The rotational power is Tw so the total power required at this instant is P=VF+T*w.
So for example if for the first case if you need 1000 Horsepower engine you will need say a 1500 Horsepower engine for the second case.