I don’t understand how spacetime has 4 dimensions. Shouldn’t it have 3? A spatial dimension, a temporal dimension and a mass/energy dimension.
In Space 3 dimensions.
Up - Down
Left - Right
Forward - Back
In Time - one dimension.
Forward only, only the rate varies.
There is no mass/energy dimension.
In this context, a dimension is an orthogonal direction along which you can move.
Orthogonal means at right angles to: Up and down is orthogonal to left and right, and both of those are orthogonal to in and out, so we say there are three orthogonal spatial dimensions. If two dimensions are orthogonal to each other, you can move along one without moving along the other: A balloon can go up and down while remaining above one spot on the ground, not moving left or right nor horizontally closer to or farther away from you as you stand on one spot on the ground.
There being three dimensions means you need at least three numbers to fix a position in space. A common way of doing it is latitude, longitude, and altitude: Latitude and longitude pick out two angles, one measured from the equator and one from the Prime Meridian, and altitude fixes a specific height above or below mean sea level. That, the two angles and an altitude, is a spherical coordinate system. You can make a rectangular coordinate system by picking one corner of your room to be (0, 0, 0), or the origin, and measuring distances north-south, east-west, and height off the floor, all relative to that corner. Rectangular coordinate systems are useful when the space you’re talking about is pretty much flat, as a room is.
With the help of the rectangular coordinate system, you can see that two orthogonal directions, such as north-south and east-west, allow you to define points on a flat plane, in this case your floor or your ceiling. Take the north-south and up-down directions and you can define points on your eastern wall, for example. One dimension defines a line, two define a plane, three define a space, and, in physics, four define spacetime. Mathematicians have more general notions, which generally don’t have anything to do with spacetime.
Time is a coordinate, a dimension, primarily because of Special Relativity, which tells us that accelerating in a direction in equivalent to a rotation in a plane defined by that direction and the time direction. This page is a good introduction to the strange trigonometry of Special Relativity.
Mass-energy isn’t a dimension. Saying it is is nonsense.
I understand the Lorentz transformation. Why isn’t mass/energy a dimension?
Dimensions relate to the minimum number of coordinates needed to specify any point within it.
As John Wheeler said “Spacetime tells matter how to move; matter tells spacetime how to curve.” but you don’t need Mass or Energy to describe a location along a world line. You can do so with three dimensions of space and the one dimension of time.
A Lorentz transformation is just a special case invariant distance formula for a non-euclidian space. preserve the spacetime interval between any two events.
Coordinates for the first point (t, x, y, z) and the second point (t′, x′, y′, z′) are the “Dimensions” with t being the proper time.
v = Relative Velocity
c = Speed of Light
γ = Gamma or the Lorentz Factor
Note how there is no mass, it is just a hyperbolic rotation of Minkowski space, because the hyperbola and not a circle is invariant under rotation between frames in relative motion with constant velocity in spacetime.
A typical coordinate system uses 3 coordinates to uniquely determine a position on a manifold. I thought determining a unique position isn’t possible in General Relativity or Quantum Mechanics so why use this kind of coordinate system? It seems you could completely describe a system by determining how long a photon takes to get from it to the observer, its mass/energy, and its time dialation
Space-time looks different to observers in different frames, but they can all calculate what observers in the other frames are seeing. That’s what Relativity means.
If you want to describe the positions and velocities of the Sun, Earth and the Moon to send spacecraft around in the solar system, how do you do that with your suggested dimensions?
Neither distance (which is what “how long a photon takes to reach it” is), energy or time dilation tells you in what direction the system is. It adds things that aren’t “of space time”, such as speed, but not the direction of that speed.
Would the change or rate of change of the time the photon takes to return from the system (and planets and moons etc.) describe well enough how to maneuver a spacecraft? Newtonian physics describes spacecraft trajectories in our Solar System well enough. I was thinking of using this coordinate system for more complex systems
Photons or other massless particles that travel at the speed of light do not experience time. In their frame of reference they are emitted and absorbed in a single event no matter how long it takes from the perspective of those of us with mass who do experience time.
What you are describing is the spacetime interval, which is the only value that observers that are causally connected agree on.
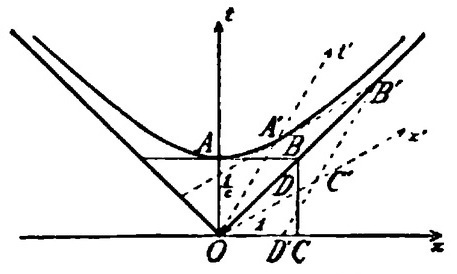
If you look at this Minkowski spacetime diagram you will notice a hyperbole, and the angles that are at 45 degrees are the path of a photon. That forward looking inverse triangle is the observers “light cone” And events that happen on that hyperbole will all seem simultaneous from the observer of that space time diagram although no events or observers on that line’s “proper time” or their that event’s local clock will tick the same.
For the most part the three spacial dimensions are stable because our universe seems to be very very flat, so the angles of a triangle will add up to 180 degrees. This would allow you to use Newtonian methods for reference from other locations, but you would need to correct for the relativistic effects of curved space time to find the most efficient path. You could use Newtonian methods at low speeds but you would have to have a lot more fuel for corrections due to the curvature.
Note that the speed of light is constant for all observers, irrespective of relative velocity. The energy/frequency will be red or blue shifted, but the speed of the photon will always be the same.
Your coordinate system isn’t even good enough for the Solar System. I can tell you that it takes 16 minutes for a photon to fly from the Sun to the Earth and back, and that it takes 24 minutes for a photon to fly from the Sun to Mars and back. Can you tell me from this how far apart Earth and Mars are? On the other hand, if I set up some coordinate system with three spatial coordinates, put the Sun at the origin, and tell you the coordinates of Earth and Mars in that system, then I can indeed tell you the distance between those two planets.