Does an hourglass weigh less while sand is falling? I mean, does it register as less weight on a scale before the last grain of sand falls? Obviously, it has the same mass either way, but when those grains are in freefall, I can’t see them as registering weight.
It should weigh less by the amount of sand falling. The falling sand isn’t exerting any force on the hourglass.
Having said that, if anyone has an hourglass and a gram scale, it should be easy enough to get an empirical answer.
Looking around online a bit, my answer isn’t (entirely) correct. What I’m reading says the hourglass will weigh the same while the sand is falling because the impact of the falling sand hitting the bottom will make up for it.
I say my answer isn’t ‘entirely’ correct because the hourglass will weigh less between the time the sand starts falling and the time it first hits the bottom. The opposite happens while there is still sand falling, but nothing remaining at the top.
https://demoweb.physics.ucla.edu/content/110-weight-hourglass
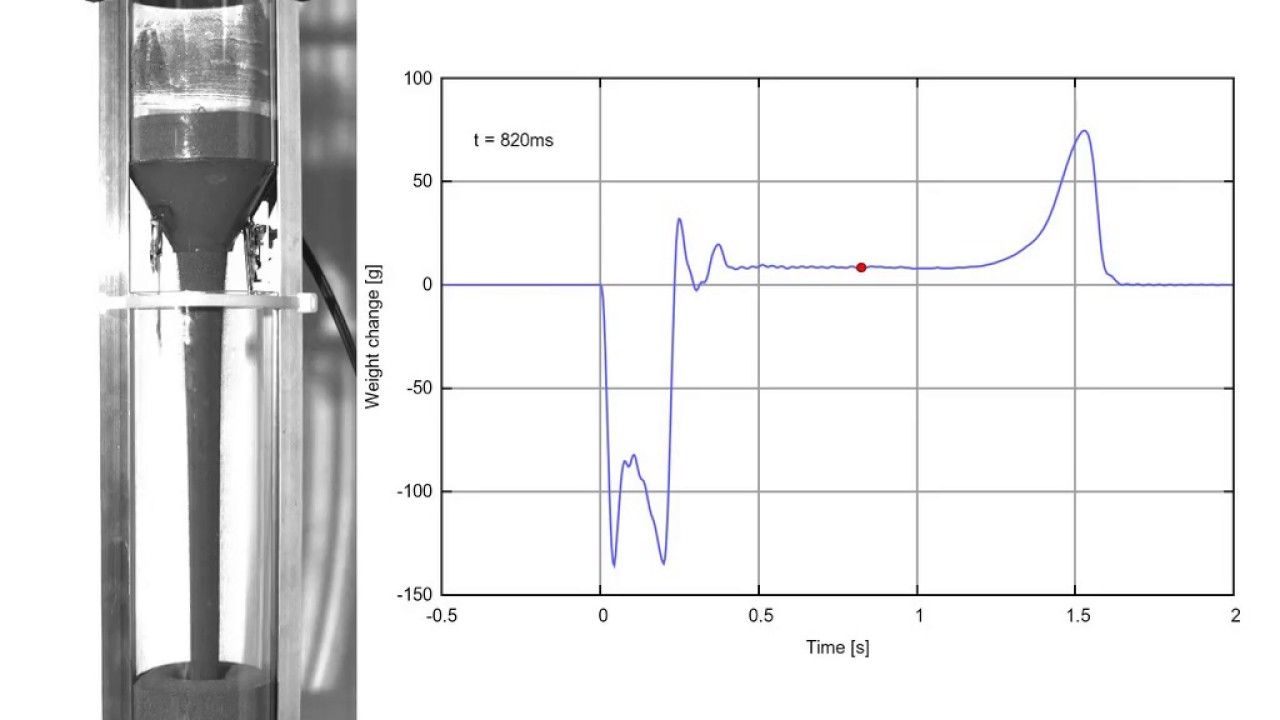
The sand in the falling column does not contribute to the weight reading. But you can easily show from Newton’s Second Law in the form F = dp/dt that the extra impact force of the falling sand exactly equals the missing weight of the total falling column of sand. Thus, while the sand is falling and impacting, the weight of the hourglass is equal to its weight when no sand is falling.
But initially, as the sand starts falling, there is “missing weight” in the column before the sand hits bottom, so the hourglass grows momentarily lighter. Similarly, at the end there a few moments while the impact force remains constant as the falling column decreases to zero,
That graph does a good job of showing that it weighs less as the sand starts falling and more as it stops. It also shows it as slightly heavier while the sand is falling, but I’m not sure what that’s about.
Also, I found this article/experiment about it.
The kinetic energy the sand gains as it falls is dissipated on impact.
Drop a ball on a scale and it will momentarily register a higher weight than what the ball weighs.
You’re right. I forgot about the whole F=MA thing.
In theory (assuming accurate apparatus etc) I believe the area enclosed by the graph above the zero line should exactly equal the area enclosed by the graph line below.
Isn’t this a variation on the birds in a truck riddle?
The birds in a truck riddle is a riddle that asks whether a container or a truck carrying birds changes in weight when the birds inside are flying.[1]
The television series MythBusters investigated the question in a 2007 episode, testing it both with a box of pigeons and again with a model helicopter. They concluded that the contents being in flight made no difference to the weight, and theorised that the downdraft of air from the wings or rotors pressed down against the base of the box with the same force as the resting bird or helicopter.[2] - SOURCE
Ultimately, scales measure force. They are intended to measure weight, a special kind force between masses due to gravity.
One assumption for weighing is that the load is at rest*. For the hourglass, the load is in motion so the forces that applied while at rest now have the additional variables of velocity and time. We know the mass didn’t change (much,lol) and it’s safe to assume gravity didn’t either.
- another assupmtion is that the scale/measuring device is at rest. For example, you can’t get an accurate weight result from a scale in a moving elevator, even though the load is stable on the scale platform.
I don’t see it as related to the birds in a truck problem. In the latter, the important point is that the birds are supporting themselves in flight by exerting downward force on the air, which transmits that force to the truck bed. There is nothing analogous to that in the hourglass.
It’s more of a frogs-in-a-truck problem. Frogs, like birds, spend some time in the air, but they do that, not by exerting a force on the air, but by temporarily exerting a greater force on the ground.
Imagine you are standing on a scale holding a lead ball. If you drop the ball, obviously your weight will go down. If the ball hits the scale, there will a momentary increase in your total weight and then it will settle back to the original. If you drop the ball away from the scale, your weight is permanently (for some value of permanent) decreased.
You guys came through. Amazing!
Nitpick The center of mass is now closer to the earth’s, thus a slightly stronger gravitational attraction, so there will be every so slightly more weight at the lower position. Though in this case that is so minor that we most likely can’t measure it, but it is there.
Didn’t Unca Cecil cover this in his column on tossing a baseball in an airplane? I’ll see if I can find it, don’t wait up.
This covers most of this discussion, just takes its time getting there.
I’m trying to work out if that’s the other side of the equation for the sand having slightly less potential energy after it falls a few centimetres, or if those two things are only coincidentally opposite.
Weight is a force. Modern balances (e.g. those made by Mettler) measure weight, and then use a conversion factor to calculate mass.
(And if you really want to get into the weeds of it, the LCD display on the balance reports conventional mass, and not true mass.)
Yes, they measure a bunch of forces, not just weight. If you mount the balance horizontally and press on the pan, it will respond though nothing is meaningfully weighed. Similarly, weighing a magnetized item (or statically charged or a large temperature difference) can be a problem since it pushes and pulls in unpredictable ways. A balance does what it can to isolate the measurement from other forces but it can’t ‘tell’ the difference between the weight/mass changing and the breeze blowing because it measures them all.
Weighing live animals is itself an art. Like the sands of that hourglass only with more skittering about and urine.
This reminds me of a joke.
“Life is like loading twice your cargo capacity onto your ship. If it’s canaries and you can keep half of them flying all the time, you’re all right.”