The version of Excel I have (an old one) evaluates -2^3 = 8 rather than -8. That is it evaluates it as if it were (-2)^3. Has this been corrected on later versions of Excel?
It correctly evaluates 0-2^3 = -8.
(-2)^3 is also -8, so there’s something else going on.
Yes (at least, it works on my up-to-date version of Excel with no problems).
IIRC operator precedence issues were a known thing in older versions. Seems it has been corrected (at least for this). Which version it got sorted out I do not know.
It gives the correct answer in the Microsoft 365 version for Mac:
And in the Excel online version:
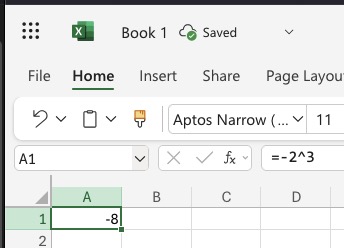
Maybe the OP meant to use an even exponent?
e.g. =-2^4 becomes 16 rather than -16)
To make it -16, you’d have to explicitly do either:
=-(2^4)- or
=-POWER(2,4)
This is still the case in recent versions: https://office-watch.com/2025/excels-order-calculation-bodmas/#h-10-2
Yeah I made a mistake. I should have used an even exponent. So to be clear my old excel evaluates
-3^2 = 9 rather than -9
0-3^2 = -9 correctly
Excel makes so many calculation errors that it should never be relied upon for scientific or engineering calculations without independent verification.
Stranger
Unary minus conventionally takes a higher precedence than exponentiation. I believe that
-3^2 = 9
is correct and is equivalent to
(-3)^2 = 9
There’s quite a good discussion of these sorts of precendence issues in this thread from late last year:
Along about post 94 it switches gears to the various forms of confusion available between monadic negation, dyadic subtraction, and the leading negative specifier of a digit string all using the “-” symbol for what are actually different ideas.
that portion, from post 94 to the end, bears directly on the OP.
That depends on what context you’re working in. In algebra, exponentiation comes first, so -3^2 would equal -9.
Cite: Wikipedia
In both Excel and software programming, I feel like the usual safest thing to do is to just be excessively explicit, adding a bunch of parentheses in every step of the equation.
I could never remember the correct order of operations to begin with (it’s not something I’ve discussed since grade school, and certainly not in adult professional life…). And even if I knew them all correctly, it’s extremely unlikely that other software (or versions) and/or coworkers or users would also share that same correct understanding, so the probability of mistakes accumulates as that equation gets shared, used, and re-used more.
Adding extra parentheses makes it clearer what your intent was (as the original equation writer), helps resolve differences between software packages, and more clearly indicates to other users & editors what the expected result should be.
Seems like an easy win?