Help me visualize this: why one spot on Earth gets more "totality time" than others in the eclipse

Factual Questions
1

From the Wiki on the upcoming solar eclipse (The USA! USA! Eclipse) [Solar eclipse of August 21, 2017 - Wikipedia]

The longest duration of totality will be 2 minutes 41.6 seconds at about 37°35′0″N 89°7′0″W in Giant City State Park, just south of Carbondale, Illinois, and the greatest extent (width) will be at 36°58′0″N 87°40′18″W near the village of Cerulean, Kentucky, located in between Hopkinsville and Princeton.[11

The moon and the Earth are both travelling, and at some point, like two people warily circling each other, one pivots in a different orientation to the other…
Something like that. Can this be explained to me without hand puppets?*
*No, I did not ask this on my wedding night.

2

The biggest difference in totality time comes from how close you are to the center of the band. The shadow is a circle that moves across the Earth, and so if you’re right at the edge of the band, only the edge of the circle will pass over you, so it’ll be over very quickly.

The other difference is because the length of totality depends on the size of the shadow, and the size of the shadow depends on the distance between the Earth and the Moon. But the Earth is a sphere, so not all points on the Earth are the same distance from the Moon. The points which are further away will have a smaller shadow, and hence a shorter totality.

So the longest duration will be at a point right on the centerline, at the point where it’s closest to local high noon, so the Moon and Sun will be close to directly overhead.

3

The shadow doesn’t move at the same speed across Earth’s surface, either. If you imagine watching the Earth from the Moon, you would see the shadow of the moon traveling at pretty much a constant speed over the disk of the Earth. Meanwhile, the Earth is rotating in the same direction as the shadow is moving.

When the shadow passes over the center of the Earth’s disk, those points are moving roughly in the same direction as the shadow, just at a slower speed. When the shadow passes over the edge of the disk, though, those points on Earth are moving almost directly towards or away from the Moon; they have very little speed in the direction of the shadow’s motion. This means that the speed of the shadow relative to the ground is faster at points near the edge of the Earth’s disk (as seen from the Sun and Moon), and slower at points near the center of Earth’s disk.

I’m not sure how this affects the duration of the eclipse, though. All other things being equal, a slower speed on the ground would mean a longer eclipse. However, the shape of the shadow on the ground changes as well (it’s more elongated when the shadow is near the edge of the disk), and that might cancel out some or all of the effect of the rotation.

4

Yet the point of greatest duration on the centerline is not the point where the shadow will be the biggest. Can you explain why? What makes the shadow “bigger” at a spot after the longest duration?

5

If I take the shade off a lamp and hold my hand out open near the bulb, it will cast a large shadow on the wall of the room.

A person walking back and forth along that wall will be in the shadow for several paces (depending on distance from lamp to wall and hand to lamp), but there is only a very small range where my hand actually obscures the bulb from their vision.

The point where my hand blocks the bulb entirely from their view is the totality money shot, tho the shadow may be on the floor, wall, ceiling, etc.

6

Keep in mind the relative size of the bodies involved… and the distances…a LOT of light is still getting “past” the moon.

This graphic really helps me make sense of it visually (keeping in mind the lack of scale…). The sun is ~400 the diameter of the moon, but is also ~400x farther away, so to us ants they appear roughly the same size in our sky, which is how in the totality path, one appears to completely obscure the other.

7

Here’s a gif of the eclipse from space. It looks at one spot, but gives a sense of how the center would be total but the fringes only partial. Now visualize that spot moving across the earth (or the earth moving under that spot) for how different areas are affected.

Phil Plait, the Bad Astronomer, is a former Doper. Too bad he left.

8

I’m not well informed enough to know the whole deal about this, but I am aware of one influential factor:

The Earth rotates once each 24 hours (approximately). That’s how long a day is. That means that if you are standing on the equator, you are traveling in a circle in space, at twenty-four thousand miles an hour.

The further north of the equator you are, the slower you are moving. Eclipses will SEEM longer, because you’ll be moving out from under the shadow more slowly, the further north you are.

9

At the equator, you’re only going a bit over a thousand MPH, not 24,000. And the shadow is moving even faster than the Earth is, in the same direction, so moving faster will actually keep you in the shadow for longer, before its back edge eventually overtakes you.

10

Chronos is a ninja typist…

Anyway, look at this eclipse track. This is computed to be the longest solar eclipse for thousands of years. Note how the track runs due east along the equator.

11

You should be able to duplicate the eclipse track with a flashlight (sun), round object (ball) and a basketball or beach ball. And three hands (or an accomplice).

12

DPRK’s link goes into more detail than any of the posts here. Go read that, and look at all the different factors they list that make that one the longest (it pretty much has all of the factors coming together to work in its favor).

13

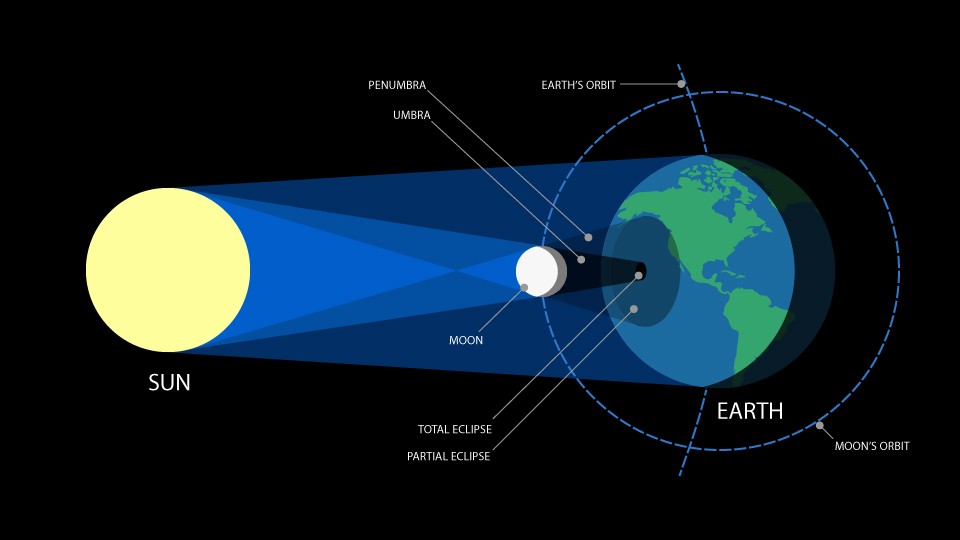
Interesting aside:

As we know, the moon is slowly spiraling out and in the far future all eclipses will be at best annular, not total. IOW, from Earth’s POV, the Moon will become too small vs. the Sun to hide it completely.

Among other reasons that DPRK’s eclipse lasts a long time is that the positions of Sun and Moon are the opposite: Seen from Earth, the Moon is about as close = big as possible and the Sun is about as far = small as possible within the current era.

Now the point: In this situation, the Moon is hiding not only all of the Sun’s bright photosphere, but the innermost layers of corona as well. Which would lead to a dimmer totality, and a smaller less impressive corona. The effect in 2186 will probably be all but imperceptible to people, but would be obvious to instruments.

If long term the Moon was spiraling in, not out, then over many millions of years the Moon would keep getting closer = bigger relative to the unchanging size of the Sun. Broadly speaking, successive eclipses would have longer totality and a period of obviously lopsided corona at the beginning and end of totality. At the center of totality the corona would be thinner and therefore spikier than what we see today.

And eventually, as the Moon got close enough and therefore wide enough, a total eclipse would really be total, obscuring all of the corona. The sky would look like truly midnight, with nothing much to look at for those few minutes until first the corona and then the photosphere came out from behind the monster-sized Moon.

I SWAG that the Moon would have to be roughly double its current angular diameter to obscure substantially the whole corona to human vision. Which means it would need to spiral in from the current orbital distance of ~240K miles to ~120K miles. The good news is that’s well outside the Roche limit Roche limit - Wikipedia, so the Moon wouldn’t come unglued and destroy the Earth’s surface before humanity gets to see total total eclipses, rather than the inferior half-total eclipses we get today.

Eventually if the Moon kept spiraling in it would get to the Roche limit. Then we’d have seen our last eclipse. Followed not too long after by a rough patch for humanity: Seveneves - Wikipedia.

All in all, it’s nice that the Moon is spiraling out rather than in. :smiley: