I don’t know if this is a correct extrapolation but.
A 1 dimensional line has one line
A 2 dimensional square has 4 lines and a single two dimensional side.
A 3 dimensional cube has 12 lines and 6 two dimensional sides.
does a tesseract have a finite, known number of lines, 2 dimensional sides or 3 dimensional cubes in it?
A tesseract can unfold into eight cubes in 3D space in the same way [-ish] that a 3D cube can unfold into six 2D squares. There are also a finite number of lines and 2D sides, but trying to visualize them well enough to count them does my head in.
Apparently there are 16 vertices, if that helps.
Wikipedia says a tesseract has: 8 cells, 24 faces, 32 edges, 16 vertices
Their cells are what you called cubes, faces are sides, and edges are lines. And vertices would be the corners.
I’ve just realized that was listed in the sidebar. D’oh!
ISTM this is not as difficult as you (and the OP) are implying.
Suppose the dimension of your hypercube is 4. Then the (0-dimensional) vertices correspond to binary words of length 4: 0000, 0001, 0011, 0010, … which you can think of as coordinates in 4-dimensional Euclidean space. [In fact, I have seen a geometry book with the entire thing illustrated, and it is not too bad, although the diagrams tend to get rather cluttered when drawing 4-dimensional figures in 2-dimensional perspective.] Counting them is easy: 2x2x2x2 = 2⁴ = 16.
Similarly, 1-dimensional facets look like 01*1 and so on, so there are 4 x 2³ = 32 of them. 2-dimensional facets have two *'s which makes 6 x 2² = 24, and so on.
Mathematical genius that I once was, I delved into n-dimensional hypercubes when I was in junior high school (7th grade, IIRC), after reading what George Gamow had to say about it in the first chapter of One, Two, Three, . . . Infinity.
Also, Edwin Abbot in his little Victorian satire Flatland describes in some detail how to generate a cube of any number of dimensions from a cube of one lesser dimensions. Thus, a 3-cube can be generated from a square (a 2-cube), a 4-cube can be generated from a 3-cube, etc.
More coming . . .
Yes, a line segment (a “1-dimensional cube”) is bounded by 0-dimensional points. A square (a “2-cube”) is bounded by line segments which in turn are bounded by points. A cube is bounded by squares, which are bounded by line segments, which are bounded by points.
And so on. It follows that a 4-cube is bounded by 3-cubes, which are bounded by squares, which are . . .
A 5-cube is bounded by 4-cubes, which are bounded by 3-cubes, which are . . .
A 20-cube is bounded by 19-cubes, which are bounded by 18-cubes, which are . . .
Thus, a cube of any number of dimensions consists, in its entirety, of a whole collection of components of all dimensions from itself on down to 0-dimensional points.
The numbers of each of those components of any n-cube are finite and can be determined. Rather easily determined, in fact, as I discovered when I played with these way back then. In fact, I developed a fairly straightforward recursive formula, similar to the formula for the coefficients in the binomial formula, where each term is derived recursively from the previous term.
More, if anyone wants me to write more about it . . .
Okay, I’ll add this, especially for the OP:
Just as a cube can be projected and drawn as a plane figure, likewise a tesseract (4-cube) can be projected and shown as a 3-d figure, which in turn can be projected and drawn as a plane figure. Here is the most common way it is projected, which I expect everyone here has seen:
I noted above that just as a cube is bounded by squares, likewise a 4-cube is bounded by 3-cubes, which are bounded by squares, etc. @Wesley_Clark, our OP, clearly understands this much, and asks:
The answers are yes, yes, and yes. And better still: If you count very carefully, you can see all the components in the above figure. So, OP, what do you see? Can you count all the cubes, squares, lines, and points just from this diagram?
ETA: To be clear: In drawing these projections, the pieces necessarily become distorted. Just as the squares that bound the 3-cube in the middle diagram are distorted and not drawn as true squares, likewise the cubes in the tesseract drawing are distorted. But, allowing for that, they are still all there and all visible. How many do you see?
@Gyrate: You too. The tesseract diagram above visualizes all the pieces for you. Can you count them all?
You and @Wesley_Clark : Once you’ve done that, your next obvious assignment: Figure out all the parts (and how many of each) in a 5-dimensional cube! Quiz on Friday!
Sure, if you take any finite number of points in Euclidean space then their convex hull will have 0-dimensional vertices, 1-dimensional edges, 2-dimensional faces, and so on.
The obvious question is how many you can have. There has to be some constraint, since for topological reasons the numbers must satisfy Euler’s formula: #V − #E + #F − #F4 + #F5 - … = 1 + (−1)d since that is the Euler characteristic of a sphere. For example, 16 - 32 + 24 - 8 = 0 in our case. Conversely, in general it gets more complicated and you have to examine McMullen’s conjecture, but in 3 dimensions it works out to V − E + F = 2, F ≤ 2V − 4, V ≤ 2F−4 being a necessary and sufficient condition, in 4 dimensions there is a more complicated condition and I’m not sure if it has been completely characterized yet (for general polytopes), etc.
This is actually kind of fun. Math was never my strong suit though, I struggled with calculus.
but using D instead of dimension, here are the figures for 1-4 D cubes.
3D cube has 6 2D sides, 12 1D lines, and 8 0D vertices for example
1D - 2 0D
2D - 4 1D, 4 0D
3D - 6 2D, 12 1D, 8 0D
4D - 8 3D, 24 2D, 16 1D, 16 0D
5D - 10 4D, X 3D, X 2D, X 1D, 32 0D
Looking at that, if N is the dimension in question, then N-1 = N*2 and 0D = 2^N. So I came up with 10 different 4D tesseracts and 32 vertices. But I was only able to guess the values for 4D and 0D based on those patterns. I wasn’t able to guess how to get the other values until I found out what they were.
Looking online, I found the values for 3D, 2D and 1D for a 5D cube.
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
So that matches the 4D and 0D values. Looking at the info, it seems like the value for the middle D values is the previous dimensions middle D value * N.
So if you want the 2D values of a 4D tesseract, its is the number of 2D values in a 3D cube*N, which is 6x4
If you want the 3D values of a 5D cube, its 8*5.
Except that I only count seven “cubes” in that diagram - one corresponding to each face of the inner cube, plus the inner one. Whereas it ought to unfold like like a Dali cross. What am I missing?
The outer cube.
PS Don’t forget to build your crooked house…
D’oh! again…
Just don’t hire Quintus Teal - his work is shoddy and may collapse in unexpected dimensions.
Take an n-dimensonal cube. To turn it into an n+1 dimensional cube, you make another copy of your cube, and then move the copy along the new dimension, and then connect every feature of the original cube to the corresponding feature of its image.
So the number of m-dimensional features the n+1-cube will have, for any value of m, can be found from the features of the n-cube. You’ll get twice as many m-dimensional features as the n-cube had, the originals plus their duplicates, and then you’ll also add as many as the n-cube had of m-1-dimensional features, because each m-1-dimensional feature, when connected to its duplicate, makes a new m-dimensional feature.
By way of example: Start with a point, a zero-dimensional cube. It has one zero-dimensional feature. Extend it to a line segment: The line segment now has two zero-dimensional features, the endpoints, and the connection between those two endpoints gives you a 1-dimensional feature, a single edge.
Now extend the segment to a square: The two endpoints double to four vertices. The one edge doubles to two edges, plus each of the two endpoints extends into another edge, for four edges total. And the one edge extends to a single face.
Now extend the square to a cube: The four vertices double to eight. The four edges double to eight, plus the four vertices extend to four more edges, for a total of 12 edges. The one face doubles to two faces, and each of the four edges extends to another face, for a total of six faces. And the one face extends to a single cell.
To a 4-d hypercube: The eight vertices double to 16; the twelve edges double to 24, plus 8 new ones from the vertices, for a total of 32; the six faces double to 12, plus 12 new ones from the 12 edges, for a total of 24; the single cell doubles to 2, plus 6 more from the 6 faces, for a total of 8, and the single cell extends to a single hypercell.
Some remarks: I mentioned in Post #6 that Edwin Abbot described, in Flatland, how to extend a cube of n dimensions to n+1. The method he gave is exactly as @Chronos describes just above. (And exactly as I would have described it.) But note something more: Note the recursive evolution of all these components. As each cube is extended to the next higher dimension, each of its components creates the new components of the next cube in a very predictable manner.
The Wiki page linked by @Gyrate in Post #2 has one diagram that illustrates this process also.
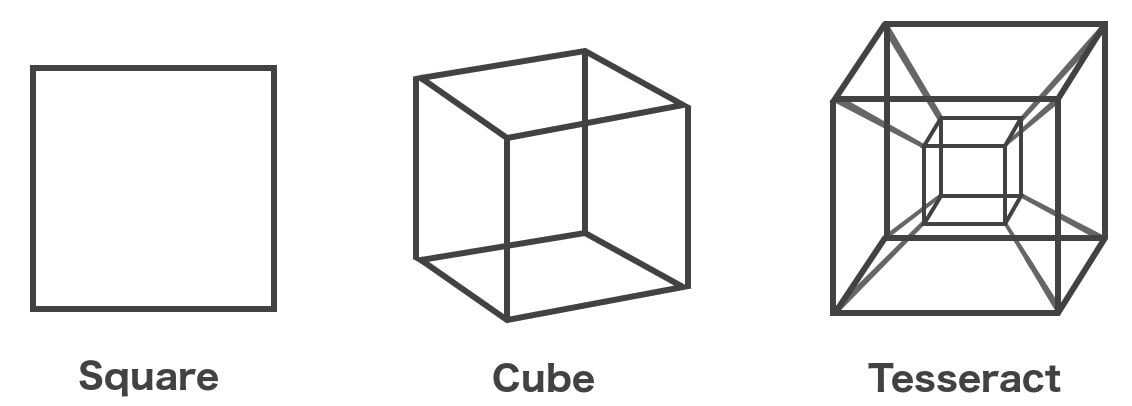
Here’s your next exercise: You can make a table showing all these numbers. On row 0, put the numbers for a “0-cube”, that is, just the number 1 for the 1 point. On row 1, put the numbers for the “1-cube” (just a line segment), that is, 1, 2 for the 1 line segment as a whole and the 2 endpoints.
On row 2, put the numbers for the “2-cube” (the square), that is, 1, 4, 4 for the 1 square as a whole, the 4 edges, and the 4 vertices.
On row 3, put the numbers for the “3-cube” (a real normal 3-D cube):
1, 6, 12, 8 for the 1 cube as a whole, the 6 faces, the 12 edges, and the 8 vertices.
On row 4, put the numbers for the “4-cube” (the tesseract), as given by @Chronos above: 1, 8, 24, 32, 16
What would rows 5 through 10 look like (for 5-D through 10-D cubes)? Just take each row of this chart and “evolve” the next row according the the pattern that @Chronos described.
THEN: When you’ve done that (okay, you don’t really have to do the entire 10 rows), and ONLY then, read on to my next post . . .
Okay, you all have a table of components for n-dimensional cubes, going up to at least 5 or 6 dimensions, right? Now . . .
Y’all remember what Pascal’s Triangle looks like, right? Reminder: Each row of Pascal’s Triangle is “evolved” from the numbers in the previous row. (Sound familiar?) There are also formulas (well, I guess just one formula) to construct any given row from scratch, from left to right, without making direct reference to the row above. You could create such a formula for the table of cubes too. But for right now . . .
Just write down the first 5 or 6 rows of Pascal’s Triangle, and set that alongside your new-fangled table of cubes. Compare all those numbers. Just sit and stare at them for while (kind of like you’re supposed to stare at those “Magic Eyes” patterns) until suddenly the picture pops out at you. What do you see?
I remember it said that 4 is one of the most interesting dimensions for constructing regular polyhedra (polytopes), because you can build up 6 of them, unlike 3 dimensions where you only get 5, 2 dimensions where it is fairly obvious that you can use any number of sides and there are no conditions, or higher dimensions where things are regular and there are only 3 possibilities.
For instance, besides the 4-cube (tesseract) you can construct a hyper-diamond with 24 octahedral facets meeting 3 at each (1-d) edge, and 6 at each vertex. One nice realization is to take as coordinates for the vertices the points (±1, 0, 0, 0), (0, ±1, 0, 0), etc., along with (±½, ±½, ±½, ±½)
The regular tetrahedron can also be generalized to any number of dimensions. We start with the 0-D and 1-D “trivial” cases (a point and a line segment) or maybe just skip those.
Then, an equilateral triangle having 1 face (the whole triangle), 3 edges, and 3 vertices.
Then, a 3-D tetrahedron having 1 3-D whole, 4 equilateral triangular faces, 6 edges, and 4 vertices.
Build a table of these, so far, like you did for the n-cubes. Compare that with the stuff you did in Post 18 above. Notice anything?
Now figure out what a 4-d regular tetrahedron is made of, and a 5-D one, and so on. You may be surprised to find that you already know these numbers.