Why haven’t any of the planets fallen into tidal-lock with the sun? Shouldn’t Mercury have tidal-locked by now? How do scientists explain away without contradicting themselves?
Mercury is sorta tidally locked—it’s in spin-orbit resonance, in part due to the eccentricity of its orbit and the weakness of tidal effects. Basically, that means it doesn’t complete one rotation per orbital period, but rather, something like three rotations every two orbits, I think.
As for the other planets, the effect is simply too weak to have much of an effect.
For the sake of discussing tidal locking (see below), I’ll ignore the phenomenon of orbital resonance (although this clearly does matter for the specific case of Mercury).
The equation for estimating how long to achieve tidal lock gives some clues. For starters, the satellite (in this case, Mercury) needs mechanical flexibility and viscosity so that its energy of rotation can be dissipated as heat when the planet is distorted by gravitational gradients. If your satellite is a giant ball of steel, it’ll take longer to achieve tidal lock than if it’s made out of, say, silly putty. As that Wikipedia page indicates, the mechanical properties of most solar system bodies aren’t well known; it may be that Mercury has uncommonly high rigidity and/or low viscosity, resulting in a long time to achieve tidal lock.
Another important issue is that tidal locking requires the existence of a strong gradient in the gravitational field. Not strong gravity, but a strong gradient. In other words, the gravitational attraction changes substantially over a relatively short distance. What’s a relatively short distance? In this situation, the best measure is the size of the satellite itself. Basically, if you want a short time to achieve tidal lock, you want the satellite’s orbital radius to be small in comparison to the radius of the satellite itself. So check out the situation for Earth’s moon:
Moon’s mean orbital radius: 384,399 km
Moon’s radius: 1737 km
Ratio: 221
Now check out the stats for Mercury:
Mercury’s mean orbital radius: 57,909,000 km
Mercury’s radius: 2440 km
Ratio: 23,733
The ratio is much, much larger for Mercury than for Earth’s moon. In other words, the gravitational gradient across the width of Mercury is relatively small (compared to the situation for Earth’s moon). Without a strong gradient, you don’t get much tidal distortion, and so less tendency for tidal locking. Absent the existence of spin-orbit resonance, It would eventually slow to one revolution per orbit, but this would take a damn long time.
Take this with a small grain of salt. I’m not an astronomer, so I can’t tell you whether the best parameter of comparison involves squaring the radii or not (it might, since gravity scales with the square of distance). But even if it does, the trend is the same: for Mercury, the gradient in the sun’s gravitational field is small compared to the size of the planet, and so tidal locking is probably going to take a very long time. This will also be true for the other planets in the solar system. Jupiter for example is huge, much bigger than the Earth’s moon, but it’s way, way, way out there; its ratio is 11,128 - not as big as for Mercury, but far, far bigger than for Earth’s moon. There’s also the question of its composition and how that affects dissipation of energy due to tidal distortion: as a gas giant it’s certainly much more susceptible to distortion than a rocky body like Mercury or the Earth’s moon, but it’s also got a much lower viscosity, so it may take much longer to dissipate its energy of rotation.
I’ll leave it to you to calculate the ratio for other planets in the solar system; I suspect you’ll find that they’re very large compared to Earth’s moon. In fact, moons seem to be the things most prone to tidal locking, according to this list.
Mercury isn’t the only one with a resonance, too. Venus also has a resonance, with the Earth. Whenever we come closest together in our orbits, she always shows the same face to us.
Tidal locking tied back to angular momentum transfer between bodies and the distance between the sun and planets is slightly further than a jaunt to the chemists.
I’m curious about these nefarious contradictions you mention though.What would you think they could be?
It appears that venus/earth is coincidental, not true resonance: see ‘Coincidental ‘near’ ratios of mean motion’ section of:
One thing to recall is that tidal forces fall off as the cube of the distance (essentially the derivative of the gravitational force). That is why the lunar tidal force is stronger than the solar, although the latter is still considerable.
Note that given enough time, which won’t happen before the sun explodes, the Earth would be tidally locked to the Moon.
But remember that there needs to be a transfer of energy here as angular momentum is preserved. In the case of the Earth-Moon system the rotational energy of the Earth is being transferred to a greater distance between the Earth and Moon but in some cases in a retrograde orbit the spin can actually increase.
Don’t confuse how things exist now as relating to what they will be. Also the tidal force is almost entirely a squeezing force and not a pulling or lifting source like is typically provided the explanations of effects like the ocean tides. The makeup of the planet directly impacts how much energy is transferred and how quickly they will lock.
The reason why tides seem confusing is that they are almost universally misdescribed even by professional scientists, and this is a well known problem in science and education.
To try an clarify some of the concepts above, due to some effects that are relativistic, mainly gravity not being instantaneous and frame dragging only an almost circular orbit will result in what is typically thought of as tidally locked like the moon is to the earth and as the earth is to the moon.
Mercury’s 3:2 resonance is just another manifestation of the same effect, but because it doesn’t have a circular orbit it will never be locked like the moon is due to how this force is transferred between the bodies.
“Spin Resonance” and “Tidal Locking” are different results of the same tidal force.
Missed the edit window
" like the moon is to the earth and as the earth is to the moon"
should be:
like the moon is to the earth and as the earth would be to the moon if the sun wasn’t going to explode first.
No, the Lunar tidal force is greater because the moon is much denser than the sun.
If the sun was denser the inverse square law results would be different because the Sun would have more mass.
But interestingly the sun does actually impact the path of the Moon about 2.5 times more than the Earth. Thus unlike many or even most other moons it’s path is completely convex related to the sun. This is why from one perspective the Earth Moon system is thought of as a binary planet, and binary orbits do typically end up being tidally locked as they tend to approximate a circular orbit.
Really it relates to the sum of the vectors across the sphere.
I’m not sure what you mean by that. What Hari Seldon said is correct - the Sun is 30 million times more massive than the Moon, but its tidal force on the Earth is weaker because it’s 400 times further away, and because tidal force scales as cube of distance. The actual gravitational force from the Sun is much stronger than from the Moon, but not the tidal force.
Given two objects of the same angular size (that is, the amount of sky that they appear to take up), their tidal forces will be proportional to their densities. But it’s pure coincidence that Luna and Sol happen to have the same angular size as seen from Earth, and if (say) you compressed the mass of Sol down to half of its current volume, it would still have less tidal effect than does Luna.
That is one of those explanations I was referencing which is wrong though.
The tidal acceleration, or lifting from the moon is 1/10,000,000 of the acceleration of Earths gravity. Even if you could shut off the Earths gravity you would never detect an acceleration that is 1 micron per second per second.
This description is a very very common but wrong explanation, and while true is so small that it does not result in effects like tidal locking or ocean tides.
This diagram is common but leads to misunderstandings, as it is not the axel difference that causes the effect but the squeeze on the sides in an angular fashion that results in the effect, specifically the forces that are tangential.
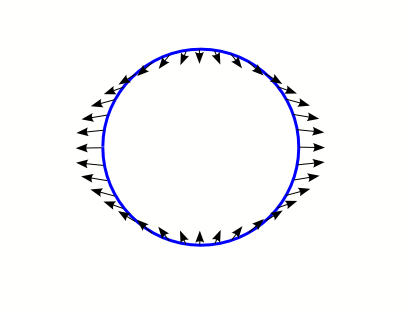
It is the tangent forces that are important, because their total effect on momentum is much larger. When combined with relativistic effects in a non-circular orbit a tidal lock of a non-circular orbit becomes the exception and not the rule.
And to be clear, this incorrect explanation of tides has been happening for literally centuries in textbooks. As an example here is a link to a reference from 1897 talking about how these concepts are almost universally explained incorrectly. So while I mentioned the relativistic effects which better model the results, the common description is incorrect even under classical physics.
As I understand it, Venus should have fallen into tidal locking long ago. But there’s some kind of secondary tidal effects on its atmosphere that keeps it rotating slowly backwards. At least that’s one theory. I’m not sure how well it’s been accepted or confirmed.
Tidal locking is really an example of spin–orbit resonance of 1:1 and due to the eccentric nature of Mercury’s orbit it will tend to a 3:2 resonance.
Mercury is locked into a 3:2 spin-orbit resonance where it rotates three times on its axis for every two orbits around the Sun.