Yes, but as you are moving forward in time, you are not occupying any space that you were previously occupying at your new space/time position.
Yes, but inside of a black hole, the t dimension is spacelike. It’s still three of one and one of the other.
I didn’t mean to do that as I was writing it, but I noticed the same thing just as I posted and found it satisfying as well. A rare case where two homographs with different pronunciations both fit! Bey-seez vs. bey-siz.
Suppose one could be inside the event horizon of a black hole and survive (perhaps our whole universe is one I’ve heard) It the time dimension is space like does that mean you can travel backwards in time inside the event horizon.
You can travel to points with a lower value for their t coordinate. Whether that ought to be referred to as “backward in time” is a matter of semantics.
There is nothing particularly special happening with time and space just inside the event horizon. They don’t “flip” in any way implied by a casual statement that they do. In particular:
No. An observer just inside the event horizon would feel time working just as it “should” in their vicinity, and they wouldn’t be able to go backwards through time.
An observer far away using a particular problematic coordinate system might calculate some kooky stuff for the inside of the event horizon, but none of it is relevant to any observation that observer could ever make.
More concretely, imagine you are watching from afar as an object falls into the simplest type of black hole. You would see the object’s trajectory never reach the event horizon regardless of how long you wait. If you wanted to describe this trajectory, you could write down the simplest sensible coordinate system for the curved spacetime and map out the object’s path using that system. Nothing overly weird happens when you do this.
Your chosen coordinate system is only relevant outside the black hole, since all trajectories you can observe stay strictly outside the event horizon. However, if you ignore this physical detail and look at the coordinate system right at the event horizon, you get some infinities (a so-called “coordinate singularity”), and if you push further to look at the behavior of the coordinates inside the event horizon, you see signs flipping between space and time. But none of that is physical. It only arises because you picked a fairly natural coordinate system for outside the horizon and then insisted it made sense for you for all of spacetime.
For the object/observer actually traveling toward the black hole, their most natural coordinate system would not show any issue at the event horizon.
As an analogy, there is an everyday example of a coordinate singularity related to navigating on the globe. If I tell you to walk directly north, you can do that up to a point. When you reach the north pole, my instructions no longer make sense, as nothing is north of the north pole. If you continue nonetheless in a seemingly (locally) straight line path, you would find that you were suddenly moving south and that your longitude value has suddenly changed. How odd!
Of course, none of those peculiarities are physical. The globe is smooth, and so was your motion. But the coordinate system chosen to talk about trajectories on the spherical globe has problems at the poles. In the same vein, the most common coordinate system used for a simple black hole has issues at the event horizon, but they aren’t physical issues, just coordinate system issues. Whether you want to label some of those issues as “time and space are flipping” is a matter of semantics. What’s critical, of course, is getting the physical implications correct.
Thank you. That makes sense and I’ve wondered about it for quite some time.
I would hope that causality is maintained in a sane form no matter what contortions space time goes through.
However you might label the axies, what we don’t want is actual loops. Or branches.
But, TBMK, frames of reference are not specifically local: they may be very difficult to reproduce exactly, but as I understand it, their values are consistent. What I am guessing (not sure if this is correct) is that, while you, on Earth, will see Bob’s starship seem to slow down as it approaches close to the event horizon, Carol is in another starship that is about to fall into a different black hole, so the time dilation for Bob and Carol will be the same and they will be able to observe each other crossing the event horizon.
Or rather, would if the event horizon lay outside the boundary where light cannot escape. As far as I know, event horizons are never outside the EM boundary, so there is no way to observe anything that happens at the event horizon.
Unless, of course, some practical way to communicate through entanglement is discovered, such that it would allow us to make such observations.
Given a black hole, there are coordinate systems that make sense and don’t have any coordinate singularities that work for the entire spacetime (except for at the actual singularity at the center of the hole, but that isn’t really part of spacetime). We could, if we chose, do all of our physics using those works-everywhere coordinate systems, even here outside of the horizon. We usually don’t, because there are simpler coordinate systems that work just as well in the region outside the horizon.
A very interesting account, thank you. But ISTM that it leaves two questions unanswered.
#1 is the paradox you mentioned – that if you were observing an object falling into a black hole, you would observe it both becoming red-shifted and also moving more and more slowly due to gravitational time dilation. Near the event horizon you’d no longer see it at all due to the extreme red-shift, but theoretically, what you would see is it seemingly coming to a complete stop at the event horizon, forever frozen in time. Yet objects can and do fall into black holes, because black holes accrete matter and grow more massive. We’ve had one or two discussions about this paradox but I’ve never seen a fully satisfactory answer.
The other unanswered question is about the inability to escape from a black hole, ostensibly because the escape velocity exceeds the speed of light. But you don’t need to exceed the earth’s escape velocity, for instance, to get arbitrarily far from it, it’s just incredibly inefficient and you’d have to expend a massive amount of rocket fuel to do it, and then you’d fall back. But there is no theoretical boundary that you couldn’t reach if you had enough low-speed propulsion.
ISTM that the inability to escape from a black hole is well addressed by the flipping of the r and t coordinates in the Einstein field equations as you cross the event horizon, where the line between the singularity and the outside world is now timelike, and no rocket of any power can get you out because “out” is no longer a spatial direction. I always thought this was a neat conceptualization. Is it wrong? Too simplistic?
This may be handwaving but it always seemed to me that this is no paradox. From the external POV, objects get “stuck” at the event horizon, but that still adds mass to the black hole system, so from the POV of the faller and of the unfallen, the black hole gains the mass of the falling object, even though the external observer might describe that mass as being at the event horizon and the falling observer would describe it as inside.
I don’t know about this statement. Theoretically, the object would indeed completely disappear from view, because it would be red-shifted. Furthermore, by definition you will not be able to observe any object crossing the event horizon.
But, now, the black hole may evaporate, so you will theoretically see particles coming from that direction, culminating in a big kaboom. What that has to do with what you threw into it is an exercise.
Correct on both counts. The “escape velocity exceeds C” explanation is a lie to children, a dodge to avoid the correct explanation. And the correct explanation is, in fact, that inside the event horizon, the singularity is in your timelike future, not a spatial direction, so “pointing away from the center” is no more meaningful than “pointing towards last Thursday”.
The part of black hole dimensionality that I have trouble thinking about is how the typical time dimension becomes spacelike. Anyone up to explaining that?
It’s basically just a rotation. Draw a compass rose on a piece of paper, and orient it so N on the rose is actually pointing north. Now rotate it 90º, so the E on the rose is now pointing north. When you do that, the N now has to be pointing in some other direction.
But of course nothing actually changes when you rotate a piece of paper with a drawing on it. There’s still only one north, one south, one east, and one west.
You can draw a conformal diagram of the spacetime in question— there is some stuff to understand, but we have one radial coordinate (of a spherically symmetric black hole) and one time coordinate, and light rays travel at 45-degree angles on the diagram. The red lines correspond to fixed radii from the black hole’s centre, and the blue lines represent constant time coordinates. No matter how you move in there, you will cross the red lines in your future.
You can see from the picture that after crossing the event horizon, the red lines and the blue lines look rotated with respect to being spacelike/timelike.
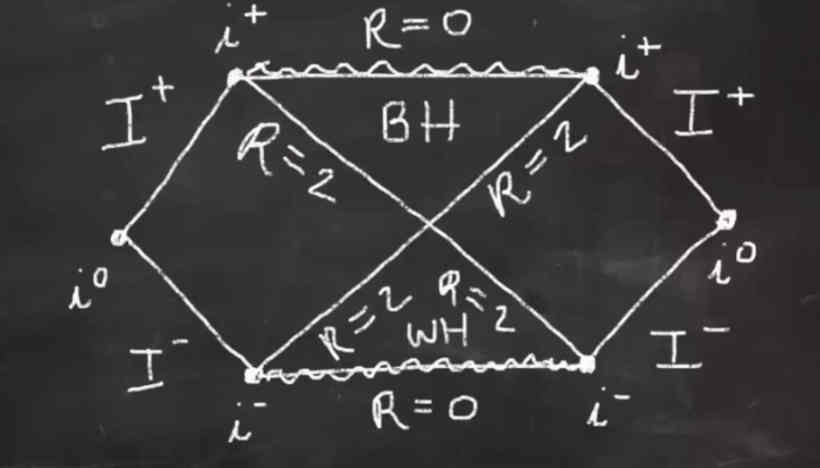
https://www.researchgate.net/profile/Claudio-Paganini/publication/328016280/figure/fig2/AS:677133512896515@1538452618941/Conformal-diagram-for-the-maximal-extension-of-the-Schwarzschild-space-time-The-blue.ppm
…Um, I don’t think we can see anything about the red lines or the blue lines from that diagram.
OK… I have a little trick to force the preview to appear:
Another diagram (red and blue are swapped here):
The Schwarzschild black hole is one of very few analytically tractable black hole configurations in GR. It is a non-spinning, non-charged, spherically symmetric, isolated, and static black hole. The instant we start throwing mass into it, several of those idealizations break, so we can’t necessarily expect to use Schwarzschild solutions to understand the growth of a black hole.
That’s the long and short of it. For something more to hang your hat on, imagine not throwing a rock into the black hole but rather a uniform spherically symmetric shell of dust concentric with the black hole. The static Schwarzschild solution would say that the dust never reaches the horizon at radius R_S, but considering the mass of the black hole plus the mass of the dust shell, there is some larger radius R_S' that will eventually be the new event horizon, and the dust will reach R_S' in finite time if we approximate the black hole as only having its original mass. So, at some point during the system’s evolution, we definitely need to update our geometry.
This isn’t a path to actually solving the system. It’s just to show that more care is clearly needed. In situations where significant mass is infalling (say, with binary star mergers), one goes immediately to numerical simulations to calculate what remote observers would see.
Yeah, I find it a little misleading to say that the escape velocity exceeds c, since there is no such velocity. Recalling the recent speed of light thread, space and time are geometrically related, and a speed greater than c is as irrelevant as “north of the north pole”. There are common diagrammatic representations of spacetime around a black hole where you could draw a line that looks like a trajectory of something going faster than c and subsequently exiting the horizon, but that’s not an explanation per se, even if it’s also not accidental.
A geometric way to state the situation is that, when caught by a black hole, your continued progress through spacetime always decreases your distance from the center.
Edited to add:
@Chronos’s version stating:
is valid, but keep in mind that the timelike-ness doesn’t have to be locally obvious. This is where I would give pause to the “space and time switch” story. It’s true that, some time in the future, you will definitely reach the singularity. But right now, time and space can look quite normal to you. The infalling observer’s watch doesn’t suddenly start measuring distance nor does his ruler measure time. But the curvature of spacetime is such that all trajectories lead inevitably to one place.