What’ the big deal about no two snowflakes being alike?
No two anything are alike at an atomic level.
Perhaps what is meant is that the crystalline structure at a higher level is different for every snowflake.
But wouldn’t he number of possible different crystalline structures be far fewer that the the number of snowflakes? If so, then wouldn’t many snowflakes be alike?
But things are exactly alike at an atomic level. Aside from energy levels, all hydrogen atoms are indistinguishable. Even at the molecular level, isolated molecules of a given compound can vary only in their energy, isotopic composition and (in some cases) chirality.
The point is that even though snowflakes are so small, tiny fluctuations in growth conditions can give rise to an almost infinite number of crystalline shapes. It may be an exaggeration to say that no two are ever alike, who knows. Probably if you grew them under carefully controlled conditions you could make identical snowflakes. But in the wild I think the burden is upon you to find two the same!
The perfect master shares his thoughts on snowflakes.
May contain transcription errors.
What’s true is that you’d have to examine quintillions of snowflakes under a microscope before you find two which are so alike that, at that order of magnification, they look alike:
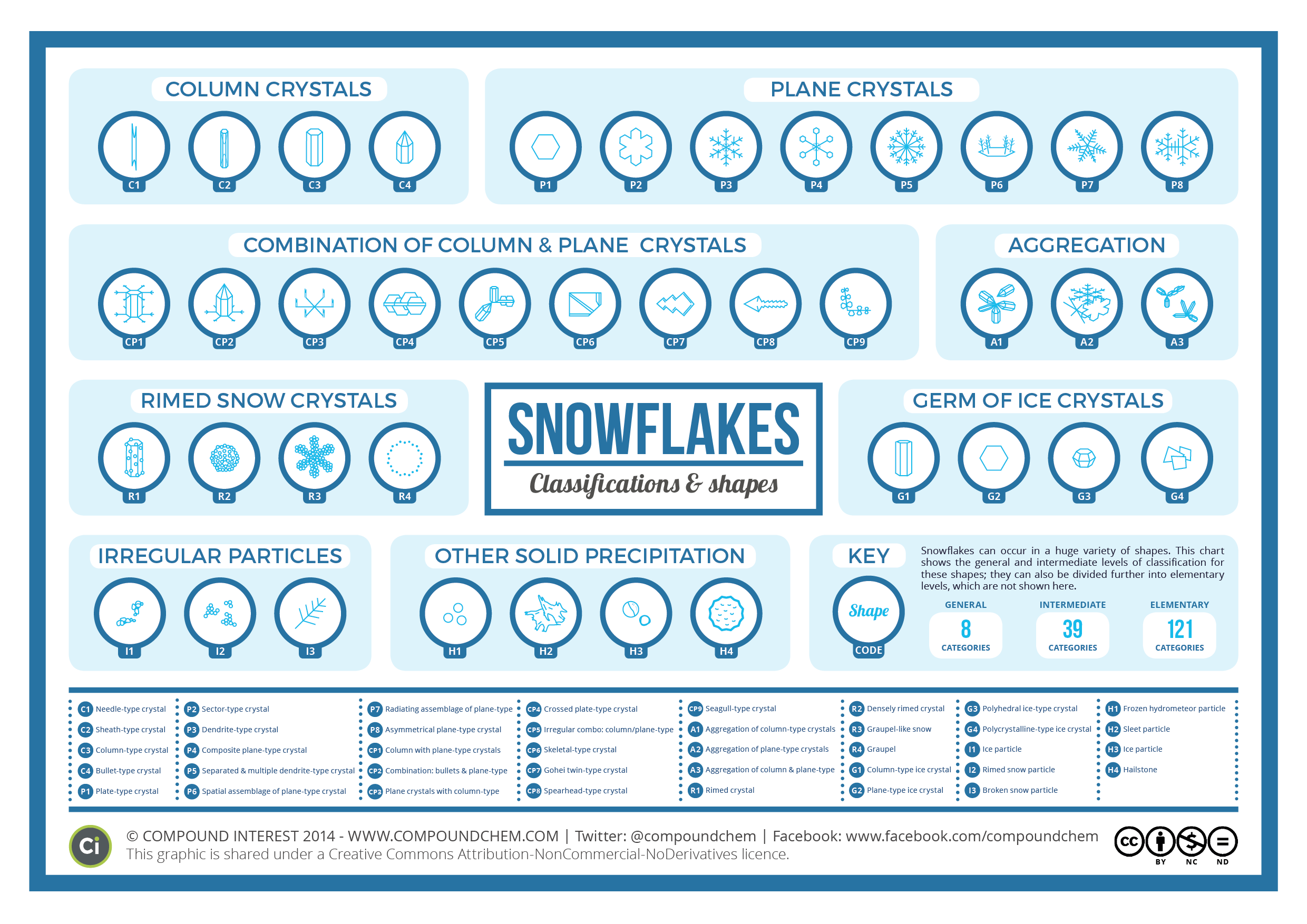
On a more superficial level, there are 39 basic kinds of snowflake shapes:
They all look the same to me.
They are all a PITA to shovel.
This is one of those factoids that is not literally true, but true on a practical level. Undoubtedly there have occasionally been snowflakes that appear identical at the level of light microscopy, especially of the simpler forms. (Even these would probably be different if you examined the arrangement of every molecule.) But there are so many possible forms that it would be virtually impossible to ever observe them (although Cecil cites a case).
The point of the factoid is to impress people about the diversity of possible forms in objects that superficially appear the same. You could say the same thing about sand grains, which would actually be more impressive because sand grains superficially appear more alike than snowflakes.
What I don’t understand about snowflakes is ‘why are they symmetrical at all?’ They have six arms, okay, but why does the arm at 12 o’clock look like a mirror-image of the one at six o’clock, and the one at ten o’clock look similar to the one at four o’clock, and so on? How does the four o’clock arm communicate details of its shape to the one at ten o’clock, and so on?
Icist.
Just found this huge image of a huge (10.1mm) snowflake from one of the links in the older post. Well worth taking a look at. (And if you’ll examine it, you’ll likely find the arms to be only broadly similar but each one different in small details.)
It’s simply what you tell kids to keep them occupied looking for matching snow flakes. In the spring you tell them 4 leaf clovers are good luck.
I think this is one of those statements people have been repeating for years but probably not based in fact.
It like “Geese mate for life” I see lots of geese where I live and I’m pretty sure a couple of them are fooling around with someone on the side.