Where does the function TREE take off?

[Lumpy]

TREE(0)= 0 (I presume), TREE(1)= 1, TREE(2)= 3, TREE(3)= ohmygod. So clearly a graphing of the function TREE would look like a nearly horizontal slope dead-ending against a vertical cliff. Somewhere between 2 and 3; but where? Is TREE still humanly cognizable at say 2.001?

[colinfred]

there is no TREE(2.001). TREE is a game played with a certain amount of colours. You can’t have 2.0001 colours.

[LSLGuy]

He’s right that TREE(n) is only defined for integer n. But I don’t think he’s talking about the right thing

Kruskal's tree theorem

[Lumpy]

@colinfred

there is no TREE(2.001). TREE is a game played with a certain amount of colours. You can’t have 2.0001 colours

Although it may not be applicable in this case, I thought that there were any number of ways of extrapolating the output of functions when non-integer N inputs are used.

[Francis_Vaughan]

@Lumpy

any number of ways

There are. Any number being possibly zero or even an infinite number. You need to pick a meaningful one. None of this is a turn the handle process. You need insight into the nature of your series to create even one. TREE is so good-awful that one doubts any extension will be forthcoming before the sun goes cold. Then again, maybe some deep insight is lurking.

One of the famous sets of extensions is of the Fibonacci series, which can be generalised in a few useful ways.

Generalizations of Fibonacci numbers

The key being the nature of the recurrence relationship defining the sequence.

TREE is not so amenable to such analysis.

[Measure_for_Measure]

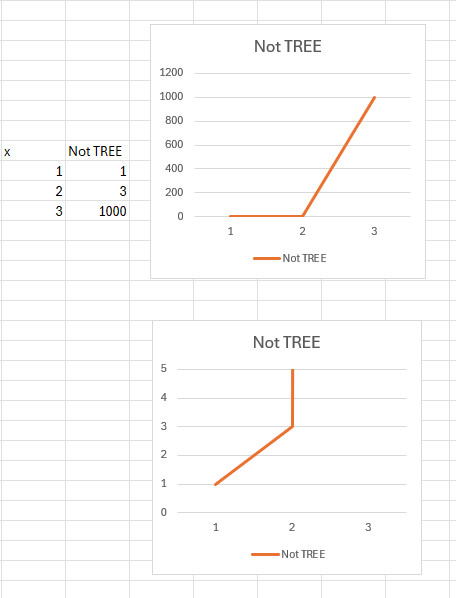
If you connected the values like they do in typical graphs, you would get a vertical line at TREE(2). To see this, consider the NotTree function with these values:

NotTREE(1) = 1
NotTREE(2) = 3
NotTREE(3) = 1000 Zowie!

Here are 2 graphs, done at different scales.

Connecting the values in this case may be somewhat misleading, but that’s what the chart would look like.

[markn_1]

What we’re looking for here is an extension of the domain of the TREE function to the reals. I think a more appropriate example is the gamma function, which is an analytic continuation of the factorial function. The factorial function is defined only on the natural numbers like TREE. The gamma function is defined on the reals (except the negative integers), but matches the factorial function on the naturals. But I don’t know if there’s any reasonable analytic continuation of TREE.

[Lumpy]

@markn_1

What we’re looking for here is an extension of the domain of the TREE function to the reals. I think a more appropriate example is the gamma function, which is an analytic continuation of the factorial function. The factorial function is defined only on the natural numbers like TREE. The gamma function is defined on the reals (except the negative integers), but matches the factorial function on the naturals. But I don’t know if there’s any reasonable analytic continuation of TREE

Thank you, what I didn’t have the vocabulary to express.