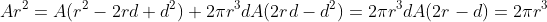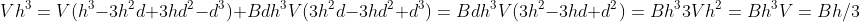Calculus of similar shapes

Miscellaneous and Personal Stuff I Must Share
1

This is something that I came up with this morning and ran a couple of examples in the shower. I haven’t seen it before. Wikipedia notes in the history of Calculus the method of exhaustion and Cavalieri’s principle, but nothing quite like this. I feel like it must have appeared at some point, though, and wonder what it might be called.

Suppose I want to find the area of a circle. I’ll call it A, with radius r. I note that I can scale the circle up and down, which goes with the square of the radius. Consider a concentric circle with a slightly smaller radius (call the difference d): the area is A(r - d)2/r2.

The difference in the area between these two is a thin strip going around the circumference. We know the area of that, too: it’s 2*pi*r*d. Just the circumference times the width. Putting it all together, we have:

Simplify:

Drop the remaining d because it’s small:

And there we have it, the area of a circle. Let’s try another; the volume of a pyramid or cone. This time the volume shrinks with the cube of the height. Consider another cone with the points aligned. When it shrinks, there is a thin slice at the bottom that represents the difference, with volume Bd. So:

Same type of simplification:

And again, the volume of a cone: area of the base times height over 3.

The technique does only have limited use; one needs some kind of similar shape, or at least a collection of shapes. It works the other way, too: given the volume of a sphere for instance, one could derive the surface area.

I guess one problem is that it depends on either limits or infinitesimals, depending on your interpretation of the “small d” I used. The ancient Greeks did use some techniques which were similar to limits but AFAIK nothing that quite resembled a small value that we can eventually take to be zero. Still, it would not shock me if it showed up in some form in Archimedes’ Palimpsest, say.

2

Yeah.

3

This seems like a type of shell integration but I admit I’m not familiar enough with calculus to say so with any certainty. I do recall learning that when successive “strips” are thin enough, they can be assumed to be rectangular because the inner and out lengths are virtually the same. Also, when I learned about shell techniques it was in the context of volumes as opposed to areas, but I imagine the concept is similar.

4

It is similar to that, but the difference is that instead of integrating thin shells/boundaries from 0-to-r or 0-to-h, I add only one shell at a time and replace the remainder with a volume/area that I already know how to compute (since it is just a scaled version of the original). In that way it isn’t quite the same as the Calculus we know, where there is an infinite sum of equally-thick strips or shells.

5

Slicing geometrical shapes into thin slices is a quite characteristic method of Archimedes: see for example the “Method of Mechanical Theorems”. In fact, I’m not sure, but isn’t that exactly how Eudoxus calculated the volume of a pyramid in the first place? There is also “Cavalieri’s principle”.

6

Mentioned in the first paragraph :slight_smile:. It’s not just the thin slices that’s at work here: it’s the idea of replacing most of the sum with something you already know, and adding just a single slice to that.

It’s similar to this method of computing geometric sums. Take:
S = 1 + 1/2 + 1/4 + 1/8 + …

We can write that as:
S = 1 + (1/2)*(1 + 1/2 + 1/4 + 1/8 + …)
S = 1 + S/2
S = 2

The infinite part just collapses away into a scaled version of the original.

Archimedes used the method of exhaustion, which is much like the modern notion of a limit. And he used many balancing arguments for computing integrals as well. But so far I haven’t seen anything that worked quite this way, though admittedly I’ve only read summaries of the Method of Mechanical Theorems.

7

Maybe I’m missing something but it looks like using the area of a circle to find the area of a circle is a bit circular.

8

It’s a good joke, but in case it’s not clear, I’m not assuming anything about the area of a circle except that it scales with the square of the radius. That’s a pretty straightforward result of being in 2D space.

I’ve realized that at least one application of the technique is very similar to something Archimedes did. Applied to a sphere, you’ll find that the volume is 1/3 of the surface area, or 4pir^3/3 (in fact the same principle applies for any regular polyhedron). What Archimedes did was view a sphere as being an infinite number of thin pyramids, with the peaks at the center of the sphere and the bases tiled on the surface. Since the volume of a pyramid (from the above) is Bh/3, the volume of a sphere is surface_arearadius/3, or 4pi*r^2 * r / 3. They’re both observations on the scaling properties of 3D space. Still, my idea above comes at it from a slightly different direction.

9

I think that you’re essentially integrating the circumference 2(pi)r and getting the area (pi)r^2.

You can do the same thing with volumes and surface area. Surface area of a sphere is 4 pi r^2, and volume is (4/3)pi r^3.

For squares and cubes, it seems to be slightly different, because you can add on to two sides of the square or three faces of the cube to make it “grow”. For a cube you’d have Volume = x^3, and surface area = 6x^2; and For the square you’d have Area=x^2, but perimeter = 4x.