I got the Barron’s AP Chemistry book for my students preparing for the test, and this question has stumped me and the PhD tutor I found. The book says only that the Ksp calculation shows that there won’t be a precipitate, and the answer is A.
But A has the charges wrong, for a start. Even if we ignore that, is there anything that shows the answer to be A? I’ve caught every book being wrong a few times.
Isn’t there a lead in to the question with the formula, ksp value, etc.?
If you assume that the “equal volumes of 2.0 millimolar solutions” refers to all chemical species represented, and assume the “Cl” should be “Cl-” and the “Pb2” should be “Pb++”, then A) is obvious. I think there is a typesetting problem, not a chemistry problem.
The ionic charges are unbalanced in © and (D).
Setting aside the typos in (A), the charges are balanced in both (A) and (B), and you must differentiate between them based on whether the lead chloride will precipitate.
It seems to me that you can get to the ion proportions shown in (B) by mixing 3 different solutions - lead chloride, potassium chloride, potassium perchlorate. So you can only eliminate (B) by knowing that there will be no precipitate.
Scratch that, I can’t count.
From a Google search, the solubility product of lead (II) chloride is 1.6 x 10^-5. If we’re mixing equal volumes of 0.002 M potassium chloride with 0.002 M lead (II) perchlorate, then the concentrations of each ion after dilution will be 0.001 M (except for perchlorate which will be 0.002 M). Thus, the reaction quotient, Q, for the precipitation of lead (II) chloride will be:
Q = [Pb2+][Cl-]^2 = (0.001)(0.001)^2 = 1 x 10^-9
Since Q < Ksp, there is no precipitation. Thus, answer choice a is the best.
I assume that the Ksp is given in a data table somewhere available to the students. I’m also assuming that there are the aforementioned typos in answer choice a.
I have emailed the student to ask if there is a Ksp in the information at the front of the test.
My other question is if the molarity values for the reactants can be on the top of the fraction in the Qsp equation. I would have thought that they were under 1. If there are just reactants added together, and there of course was no product already made when they met, are their values on the top of the fraction (over 1) on the right side of the equation?
I don’t think any of this this is relevant.
Surely the number of ions shown in the flasks represents the stoichiometry. (C) and (D) are eliminated quickly because the ionic charges don’t even balance. (B) is eliminated because there is no possible way to get those proportions of ions along with a PbCl2 precipitate from any combination of equal volumes of equal-molarity solutions.
The Ksp is for the dissolution reaction, not the precipitation reaction (i.e. the reverse of the dissolution reaction). That is, for:
PbCl[sub]2(s)[/sub] –> Pb[sup]2+[/sup]sub[/sub] + Cl[sup]-[/sup]sub[/sub]
Therefore, the K expression for the dissolution has the two ion concentrations in the numerator because they are products in the dissolution reaction. The K expression for the precipitation reaction would have the ion concentrations in the denominator (with 1 in the numerator) because they are reactant in the precipitation reaction. However, the value for K for the precipitation reaction would be equal to the inverse of the value of K for the dissolution. So the math works the same regardless of which way you write the reaction.
If this link works, here’s the probable formatting of the question. Information followed by several questions related back to the information.
So, please correct me where I’m wrong here in this explanation, as I would currently give it to this stumped kid.
The Ksp is for the dissolving of the supposed solid. So we look at the reverse reaction, assuming that there might be some solid. The Ksp is now applicable for this version of the reaction, not for the one with the aqueous ions on the left.
We have the reverse reaction as PbCl2(s) <–> Pb+2 + 2Cl-. Put in the math for the Qsp expression, and we get Qsp = (.001)*[(.001)2]^2. This gives 4.0E-9, which is a smaller number than the Ksp of 1.6E-5. The reaction at that dilute solution wants to run in the direction of forming aqueous ions more than it does the direction of forming solid, buy about a factor of 10,000. There will be no precipitate.
The missing charges in A are just typos.
You should not multiply the chloride concentration by 2. If the source of the chloride ions was the solid lead (II) chloride dissolving, then we would need that 2 there because there would be twice as many chloride ions dissolving into solution as lead (II) ions. However, the source of our ions is not the solid but rather two other solutions with ion concentrations of 0.002 M. Once accounting for dilution that occurs when we mix the two solutions, each ion concentration in the mixed solution is 0.001 M. This then means that Q = 1E-9 rather than 4E-9.
The remainder of your explanation looks good to me.
Sent from my Nexus 6P using Tapatalk
I feel a bit dumb about that 2 multiplier. Thanks!!
Now, I know what my teachers went through when they told us to correct something in the textbook.
My school often used the same math & science books for several years. The teacher knew the textbook and homework problems extremely well.
Corrections were often already penciled in by students in prior years.
So the OP’s main question was whether a precipitate forms or not. No ? Because what forms instead ? A does not show anything the lead is doing.
What it forms is the lead peroxide radical right ?
I’m not sure that you’ve got the correct Ksp formulations… Won’t ClO4- break apart very fast … isn’t Pb a catalyst to breaking down ClO4- ?
I think the books writer/editor had started to write this question, got stuck on it, being unsure of what to do, and forgot to fix it… Looks to me like they were going to change the precursor part of the question… He might be in unsafe territory due to the number of possible explanations for why no precipitate forms… Its not the intent of the question to test the students memory of experience - as in knowing the emperical result?
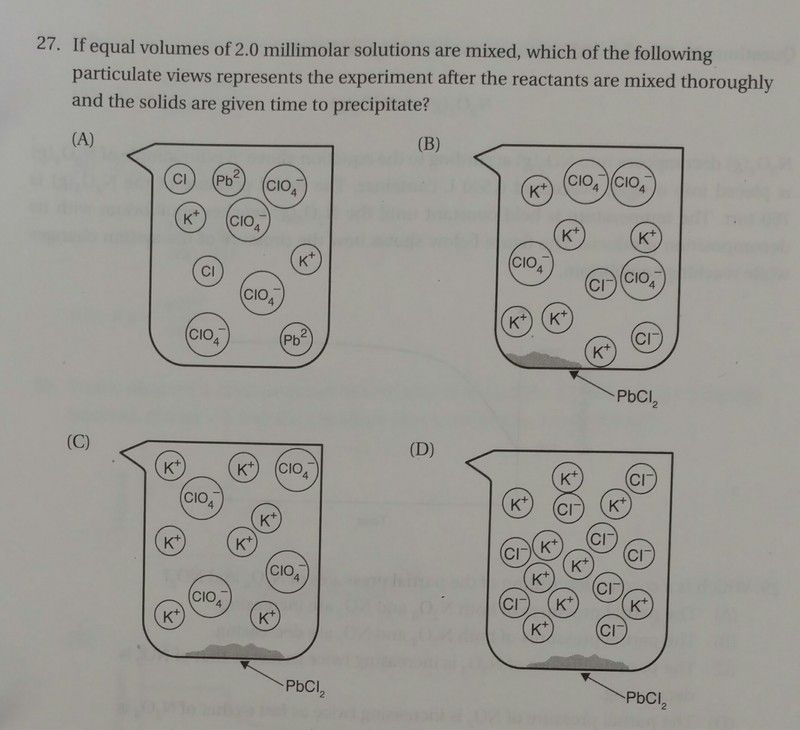
Nothing forms. That’s the whole point of the question. The question is testing whether or not the student recognizes that no reaction occurs (i.e. that no precipitate forms because the concentrations are too low to cause the precipitation).
That’s because the lead ions aren’t doing anything (in the sense that they’re not reacting; obviously they’re continuing to move around randomly due to Brownian motion).
I don’t know why a peroxide would form. Lead (II) chloride, lead (II) perchlorate, potassium chloride, and potassium perchlorate are all stable compounds (certainly more stable than a peroxide would be).
Not that I’m aware of. Perchlorate is stable in aqueous solution.
I doubt it. If the intent were to assess the student’s memory of whether or not lead (II) chloride is insoluble, then either no concentrations would be given or the concentrations would be much higher (closer to 0.1 M). At those concentrations, a precipitate would indeed form. However, the concentrations are probably given for a specific reason: so that students can perform the Qsp calculation. Presumably the Ksp is also included in the test somewhere for the students to compare to their calculated Qsp.
It looks to me that there was simply an error made in sizing the circles such that they don’t cut off the superscripted charges. With the assumption that the Ksp was given in some data table (reasonable considering that this was taken from a practice test) and the assumption that the circles surrounding the Pb[sup]2+[/sup] and Cl[sup]-[/sup] ions are simply formatted too small and therefore cut off a portion of the text, answer choice (A) is best.
Even without making these assumptions, I would still argue that answer choice (A) is best. Let’s assume that the precipitation of lead (II) chloride goes to completion. That is, lead (II) chloride precipitates until either the lead (II) ion concentration or the chloride concentration is zero (or both, if they’re in a stoichiometric ratio). We’ve mixed equal quantities of 0.002 M Pb(ClO[sub]4[/sub])[sub]2[/sub] and 0.002 M KCl. This means that immediately after mixing and just before reaction we have the following concentrations: [Pb[sup]2+[/sup]] = 0.001 M; [K[sup]+[/sup]] = 0.001 M; [ClO[sub]4[/sub][sup]-[/sup]] = 0.002 M; [Cl[sup]-[/sup]] = 0.001 M. After the reaction (as much PbCl[sub]2[/sub] has precipitated as possible), the concentrations are now: [Pb[sup]2+[/sup]] = 0.0005 M; [K[sup]+[/sup]] = 0.001 M; [ClO[sub]4[/sub][sup]-[/sup]] = 0.002 M; [Cl[sup]-[/sup]] = 0 M. That is, all the chloride ions have precipitated and half the lead (II) ions have precipitated. So if our assumption that the precipitation occurs is correct, we need to look for an answer choice where we have X lead (II) ions, 2X potassium ions, and 4X perchlorate ions. There is no such picture shown.
In (D), the perchlorate ions have simply vanished from solution, thereby violating mass balance. In (C), the potassium ion concentration is higher than that of perchlorate. In (B), we have no lead (II) ions left in solution, fewer perchlorate ions than potassium ions, and some chloride ions left in solution. Whereas in (A), we have the exactly correct ratios of ions (albeit with incorrect charges on the lead and chloride ions). Occam’s Razor suggests that it’s simply a formatting error.
In case anyone cares, yes, the Ksp was given, but before the previous problem. So both the student and I were too dumb to look back for given information. I’m really surprised he didn’t, since he had been doing the problems, but I should have, too.
So I’m convinced now that the Qsp calculation is what gives the lack of precipitate. They even made the concentrations so low that if you multiply by 2 on the chloride ion, you still get the same answer of there being no precipitate. They also made the math possible for mental math, as you can just add up the E-3 numbers and get E-9.
So Qsp is not remotely strong enough to force a precipitate, and any solid that managed to form would immediately dissolve.