Not a hypothetical like a map line or a “longest possible sea voyage”. Something like a road, railroad track, power lines, data cables, pipeline, logging trail, canal, etc… Straight-by-compass-direction will be included even though it wouldn’t be a great circle, and changes in vertical elevation won’t matter since I’m thinking in map terms here. Record book asterisks will be noted for lines with significant dog-leg deviations. Participation prize will be awarded to discontinuous (i.e. boundary markers) lines if every marker is line of sight with the ones next to it.
Great Nullarbor stretch of Trans-Australia Railway is 297 miles dead straight. Elevation changes, I think, and obviously it follows the curvature of the Earth.
How about the beampaths of LIGO? They’re 4km in length, under ultrahigh vacuum, and can detect changes in beam length on the order of 10^-4 the charge diameter of a proton.
Does the line have to be permanent? I’m thinking you could get some awfully long contrails.
Does submarine cables count ? If so then :
“SEA-ME-WE3 or South-East Asia - Middle East - Western Europe 3 is an optical submarine telecommunications cable linking those regions and is the longest in the world. ”
From : SEA-ME-WE 3 - Wikipedia
LIGO is hereby presented with a Special Lifetime Achievement Award for being the longest absolutely straight line.
If you can cite stretches that don’t have any detours, curves, etc., yes.
Nazca Lines came to mind, but apparently the longest is 1200 feet.
I can’t tell if it’s really dead straight, but the McMurdo-South Pole Highway has a section (going over the Ross Ice Shelf) that appears to be pretty close, and around 500 miles.
The shelf is pretty flat and so the road has no mountains or valleys to avoid, though it must make some small deviations to bypass large crevasses.
Doesn’t this hinge on how you define “straight”? Even a nominally straight road or cable has subtle wiggles and irregularities. And a laser beam will be made non-straight by thermal refraction, gravity, etc.
How straight is straight?
US-Canada border is noted for having the longest straight border on land, in the world. See this NYT post about it: The Not-So-Straight Story of the U.S.-Canadian Border - The New York Times
They note the border zigzags a few hundred yards north and south of the parallel. But, per the wiki: Canada–United States border - Wikipedia , it’s kept clear of vegetation, and is mostly straight for some 1400 miles or so. Well, it parallels the 49th parallel.
Anything that is straight as the photon flies might be as straight as can be defined as straight. If it is flying a geodesic in space time it gets hard to say it isn’t straight, even if an external perception is of a curved path. After all, whose frame of reference do you believe?
This map is not intended to show the actual path of the cables on the ocean floor, but it seems likely that one of the trans-pacific cables has a straight section several hundred miles long, if not thousands.
I’m dubious about the submarine cables, which—unless trenched—would naturally flex, settle, and bend to accommodate lying on an irregular surface (the sea floor). Any time one crosses the side slope of a seamount it would sag into a gentle curve. And then there’s currents.
Geodetic Surveys were made to cover large portions of the earth in the 19th century. They made extremely precise measurements over long straight lines. The most famous, arguably, were the surveys of India, The Great Trigonometric Survey. It was started by William Lambton in 1802. He was succeeded by George Everest, after whom Mount Everest was named (as a result of his survey work) . He was succeeded by Andrew Scott Waugh, who was, in turn, followed by James Walker, who completed the work in 1871 (!!). They typically surveyed in equilateral triangles with a baseline of 7.5 miles, all in a straight line.
The book The Great Arc by John Keay is devoted to these surveys.
Inspired by these efforts, Jules Verne imagined a similar survey of Africa, which he wrote a fictional work about, Meridiana (AKA The Adventures of Three Englishmen and Three Russians in South Africa), written in 1872, just after the completion of the Indian survey. I don’t recall the length of the baelines in Verne’s work
One attempt to measure a very straight line was made by the Koreshans in 1897 on the beach at Naples Florida, in an attempt to prove that the earth was round, but concave, with us living on the inside. They extended a line four miles along the beach and claimed that they saw evidence of “upward curving”, which proved their point. (They had previously performed similar experiments elsewhere, as at the Illinois Drainage canal, but this was longer).
I don’t know how straight it is - but what about something like the Kola Superdeep Borehole? It’s over 7.5 miles deep and I would think is “mostly” straight. There are some longer oil wells - but oil wells routinely curve, sometimes quite a bit - so I’m sure they’re not as straight as Kola.
Note that only the meridians and the equator are geodesics or the equivalent of a “straight line” on a curved surface.
For every line of latitude that is not a pole or the equator is curved as is any more general “rhumb line” (line that crosses meridians at a constant angle)
If one is at say 10 degrees north and facing directly East and started walking, one would need to turn left all the time in order to not cross the Equator.
Note Proposition 6.17 on this differential geometry course (PDF) will be the easiest to test with I know of for surface features at least.
It is Clairaut’s relation and works with any smooth surface of revolution which will remove the problem of the Earth not being round. It will show if a course is locally geodesic, but I can’t explain why the US and Canadian border etc…are not straight lines without math.
Geodetic surveys typically seek to establish consistent coordinate systems and do not care about “straight lines” As any line of latitude is by its very nature a curved may be problematic.
This is where the OP needed to bound the conditions better in order to reach a consensus.
The OP explicitly allows “straight by compass” paths even though they aren’t great circles.
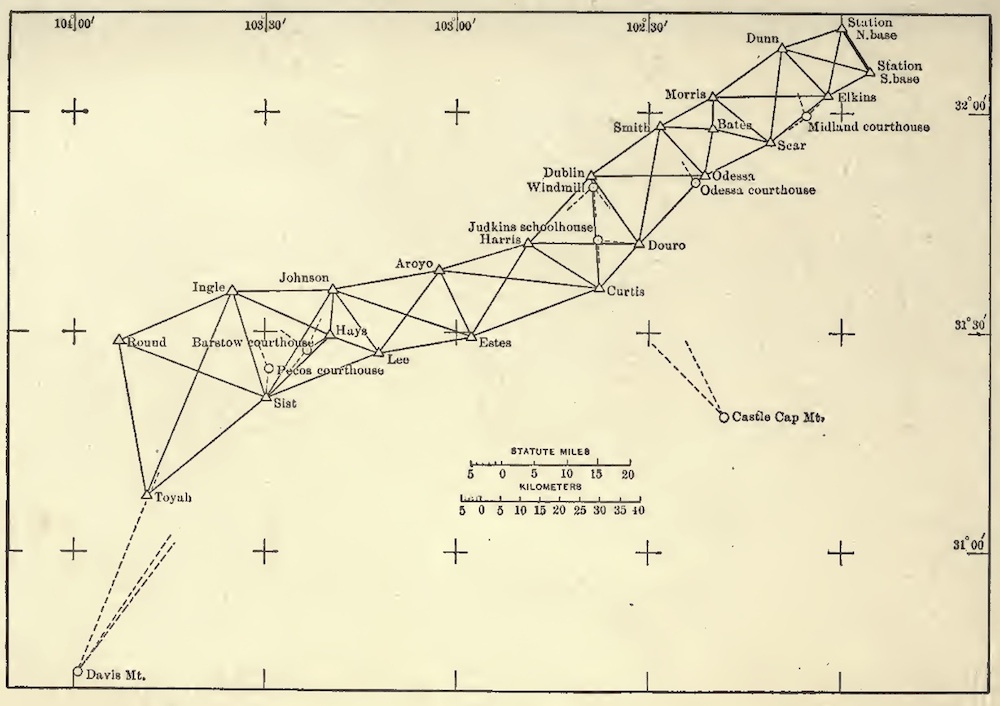
That opens up more possibilities as loxodromic paths can even be spirals but I was mostly trying to point out that referencing geodetic surveys, while in a geodetic survey any line between two stations is considered to be spherical and not straight like in plane surveying which is accurate enough at local levels. As it is not really possible geodetic survey locations are not “in-line” as it would be pointless thus they are chosen due to convenience and practicality.
Here is an example historical map, showing how those stations wouldn’t be straight on a line.
I think the OP intended mostly loxodromic so here is my entry for roads Saudi Arabia Route 10
Most road builders explicitly avoid being straight for that long due to safety issues and driver attention even if it is practical. I think the straight section is about 160 miles long.
The border between Namibia and South Africa/Botswana has a 444-mile-long north-south section which appears from Google Maps to have a fence and/or dirt track along almost all of it. Although if you zoom in it appears not to be a perfect north-south line all the way, even though it was defined by treaty to be 20 degrees east longitude.
The northern section of border with Botswana, further east, is over 250 miles long, dead straight and seems to be physically marked.