Negative mass is the stuff invoked by physicists to keep wormholes open and make warp drives work. If it exists, what kind of properties would it exhibit on Earth’s surface? What energy conditions does it violate?
Just judging from F = Gm1m2 /r^2, it does seem like it would go flying away from the earth when one of the m’s goes negative.
But F=ma, so you would get another negative in the equation and the negative mass would actually still accelerate towards the earth.
Nope Folly. The acceleration is a vector in the direction of the force.
That’s very positivemass-centric of you.
What the properties of “negative mass” would have are yet to be determined. The property of never existing is most likely.
However, if something is invoked that can hold open a wormhole, it would have to do so by repelling normal matter and energy, and by being repelled in return.
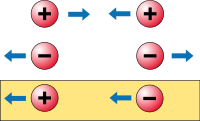
From NASA, slide 6.
Negative mass still falls “down” in a
gravitational field• Force of gravity is opposite:
F = GmM/r2
• so when m is negative, gravity pushes
• but
• When you push on negative mass it moves
toward you
• So negative mass still is attracted downward
(toward positive mass)
Gravitation is not a force as much as it’s geometry. Photons and other massless things move in straight lines through space-time. Gravitation is the description of what straight is. Massive objects try to move in straight lines through space-time, but their mass gives them inertia, which prevents them from going straight.
The interesting part of negative mass is how it affects space-time. It bends space-time opposite of positive mass. That is why negative mass is needed to stabilize things like wormholes, which would otherwise collapse upon themselves.
In simple Newtonian terms, think of two particles with equal and opposite mass. The acceleration of the negative-mass particle will be toward the positive-mass particle. The acceleration of the positive-mass particle will be away from the negative-mass particle. This leads to a “race” condition where the two accelerate without bound!
This diagram illustrates this hypothesis, showing the gravitational interactions between positive and negative masses:
The consensus seems to be that this runaway acceleration can’t be physically possible, or else you could use it to create a perpetual motion machine! It’s the only type of mass interaction that doesn’t have an end-state.
These guys claim to have made supercold rubidium atoms exhibit the behaviour of negative mass, but my understanding is that this is not actually true negative mass in the context of either general relativity or Newtonian physics. Interesting, though:
Applying the diagrams to the OP’s question, a negative mass particle would seem to fly away from the Earth because the difference in masses makes it appear that the Earth doesn’t move. In the same way that the Earth moves up only imperceptibly toward a positive mass particle falling toward it.
How do we know that it’s F = ma and not F = |m|a until we have some actual negative mass to work with?
Well, either the OP is answerable based on the equations we have or its unanswerable I guess.
The actual equation is F = d/dt p. That is, force is the time-derivative of momentum.
If this imaginary particle is much smaller than the Earth, and has positive inertia, it will still move downwards. If you think about the curvature of spacetime, the positive gravity of Earth is vastly greater than the negative gravity of the negative mass particle, so the negative mass particle would still be attracted towards the Earth - but just not quite as strongly.
But if the negative mass particle also has negative inertia, then it will react to gravity in a completely different fashion. Pull on it, and it will move in the opposite direction. I suspect as well that matter made with negative inertia would fly apart immediately, so it is entirely non-physical.
I think it’s because we have both solid theoretical and empirical reasons to believe that negative mass should interact with other masses in just the way illustrated in the above diagram, plus experimental observations like the one with the rubidium atoms. That being the case, conservation of momentum and energy requires that negative mass possess negative momentum, so that if for instance you have negative mass chasing positive mass in never-ending acceleration, the total energy of the system has to be conserved. Thus negative mass must be -m, not |m|, in formulas for momentum and kinetic energy.
I understand, but the question remains because momentum is also signed. Actually it’s a vector, but unless we start talking about imaginary mass, I assume the momentum vector points either in the direction of the motion to opposite to it. We don’t know which way it points for negative mass. Again the question reduces to does gravitational mass equal inertial mass or does the absolute value of gravitational mass equal inertial mass.
It’s even more complicated when dealt with properly; see four-momentum.
Mass is the invariant portion of the four-momentum.
At a more abstract level, conservations of energy, mass, and momentum are due to the “translational” symmetries of the four-momentum. Inertial, gravitational, and moment masses are necessarily identical.
It is answerable depending on what type of negative mass we are talking about.
As it is hypothetical, and almost certainly will never exist in any fashion, it is unanswerable.
If you assume that negative inertial mass is a thing, then you get one answer. If you don’t think that negative inertial makes any sense, you get another.
Negative gravitational and positive inertial is pretty straightforward. Just means it repels and is repelled by normal matter. It could have all other interactions being more or less the same or equivalent. I’m not sure how this breaks the laws of conservation of momentum, and it really just means that the equivalence principle needs to be updated to take into account the observed properties of negative mass.
Negative inertial mass is what doesn’t make sense and creates situations where you can make perpetual motion machines. If I have to decide between the equivalence principle and the laws of thermodynamics, I’m going to side with thermodynamics.
Now, if it does have negative inertial mass, that makes it pretty much useless. If it has no other charge, then it means that it will repel itself, and you could never have a chunk of it. If it does have a charge, whether electrical or some other self interacting property unique to it, then that means that that charge ends up being condensed. If it had a positive electrical charge, then it would repel and be repelled by other negative mass with a positive electrical charge, and its negative inertial mass would mean that that repulsion actually cause them to come together. This would continue until there was just one giant ball of charge. Assuming that it is stronger than gravity, then it would just keep building up indefinitely, there would be no limit for its size, other than the amount of charged negative mass matter for it to suck up. All negative mass matter within its light cone with that charge will be drawn towards it. All normal matter will be repelled
So, if it has no form of self interaction, then it would be dispersed more or less evenly through the universe. If it does have any form of self interaction, then it would clump up to where there was just one example of any particular charge within the observable universe.
You couldn’t have complicated bonds, like between a positive and negative charge, as they would be forced apart by their attraction on negative inertial mass, and you certainly couldn’t have anything like the strong force, with 3 different charges.
So, you could never have a ball of negative mass.
I have no idea what formulas you’re applying to get this result. Multiplication doesn’t work like that.