Well, I regret mentioning ChatGPT now. I should have said “I have reason to doubt the comic’s premise, but I’m not an expert. Are small 1 farad capacitors as inherently dangerous as this comic makes them out to be?”
I don’t think the other people are recoiling because the device is dangerous. I think they’re recoiling because it’s unexpected, extreme, and surprising.
Interesting, so now it checks against trusted sources, as defined by humans.
Obviously it’s an improvement and mostly negates my initial objection, but wouldn’t it be better to just check the sources directly?
It’s an amazing time saver. And if what I’m doing is critical, I abso-damn-lutely will fact check it, but I’ll go in armed knowing where to fact check when I might not have before.
Fair enough
I interpreted “Be careful!” and “Put it down!” quite differently than you did. ![]()
ETA:
I should have just checked Explain xkcd first.
Cueball claiming to have a 1-farad capacitor elicits unwarranted panic from Megan and White Hat, who fear that it could be very dangerous. In reality, any hand-held 1 farad capacitor should have a very low energy limit and therefore not be in any way dangerous.
Any answer returned by a LLM should automatically be preceded with the disclaimer “I am told that…”
To kind of get back to the original cartoon, I have pondered from time to time why the gram is so dinky. I mean, the meter is a human-sized unit for dealing with objects as is the liter but nothing but a few drugs are sold by the gram.
Yes, the gram was originally defined as the weight of 1 cubic centimeter of water but if it had been decided to have it as the weight of 1 cubic decimeter of water instead, a liter would weigh a gram and you just shift the prefixes by one notch. A good-sized hamburger would be 250 milligrams instead of 250 grams, for example.
Because it’s convenient for chemistry I’d say, they weren’t using kilogram amounts of materials in the lab.
Light as grams are, they’ll still a lot larger than grains
As one might expect, the volume also goes with the square of voltage. To double the voltage tolerance, you need to double the dielectric thickness. But that then halves the capacitance. So you then need to double the area to maintain the same capacitance. So 4x the dielectric volume for 2x the voltage. But you get 4x the energy so it’s ok.
The bit I don’t understand is that, no matter which version of metric you use, MKS or CGS, you’ve got a “base unit” (the kilogram or the centimeter) with a prefix. Whatever the base units are, whyever they’re convenient, they should be the ones that all the prefixed units are based on.
Personally, I favor the meter-ton-second system. That way, all of the base units are unprefixed, and it retains the useful feature that one cubic length-unit of water masses one mass-unit.
So for any given capacitor technology, the energy density (energy per volume) is the same. But as technology improves, so does the energy density.
Unfortunately convenience takes a back seat to precision of measurement. For example it was for some reason easier to specify the exact weight of a milliliter of water instead of a liter.
The only times I bought grains of anything they were encased in brass and had a couple of other parts that made the grains inside moot, except for trusting the manufacturer had measured it right.
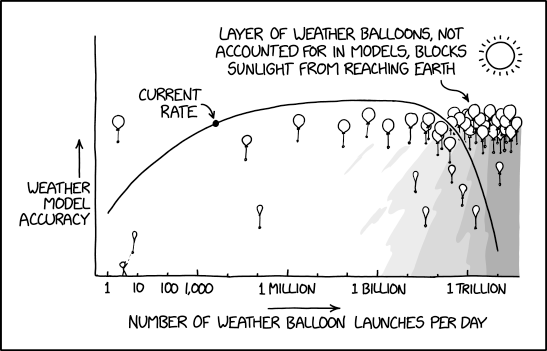
“Once you add the balloons into the model, it makes forecasting easier overall–the forecast is always ‘cold and dark, with minimal solar-driven convection.’”
Heisenberg strikes again!
![]()
Ladies and gentlemen, Randall Munroe solves AGW once and for all. And using existing tech no less.
His name will go down in the annals of human history alongside such great thinkers as Aristotle and Einstein.
Is his “current rate” indicator still valid, given the mal-administration’s cuts to NOAA & NWS?
The silly part of course is that weather balloons have a finite lifespan, primarily due to loss of lifting gas as the balloon undergoes thermal cycles of expansion and contraction. Superpressure balloons suffer less from this but weeks or months aloft is still a significant achievement.
It’s been suggested that microscopic glass hollow spheres filled with dry nitrogen could behave as high-altitude aerosols with persistence times in the decades. But that would be a geoengineering feat no one is brave enough to try.
Right, which is why the horizontal axis is rate of launching weather balloons, not cumulative number launched. Given any rate of launch and the lifetime (and the size of each balloon and the surface area of the Earth), you can calculate the equilibrium level of balloons currently in the atmosphere. Launch them at a high enough rate, and the sky will remain blanketed with them, even as the old ones wear out and fall back to ground (and new ones are launched to replace them).