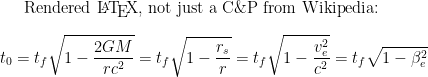Gravity and time dilation

Factual Questions
1

I have a rough understanding that clocks run slower the deeper you are in a gravitational field. There’s even a simple equation for the situation of a spherical nonrotating mass, which I will link to because I don’t know how to enter formulae: wikipedia for gravitational time dilation.

Now I can plug numbers into a formula with the best eighth graders, so to me it looks like tf/t0 for Earth’s surface (M = 5.972e24 kg, r = 6.371e6 m) is 1.000000001. So for every second on Earth, 1.000000001 seconds pass at infinity, assuming various things.

Standing on the Sun (at night, of course, for M=1.988e30 kg and r = 6.957e8 m) gives 1.000002. So for every second on the Sun, 1.000002 seconds pass at infinity. The Sun is a deeper gravity well, so time goes slower there than it does on Earth - if they were both isolated nonrotating masses, anyway.

But here’s a twist: if I check on tf/t0 for the Sun but at the radius of Earth’s orbit (so M = 1.988e30 kg but r = 1.49e11 m) I get 1.00000001. That’s seven zeros before the 1, not 8. So it appears that the time dilation that you feel on the surface of Earth, caused by Earth’s gravity alone, is less than the time dilation you would experience at Earth’s distance from the Sun, caused by the Sun’s gravity alone.

This seems odd to me, because the local acceleration due to gravity here is 9.8 m/s^2 due to Earth but only (looks up stuff) 5.9e-3 m/s^2 due to the Sun. So, naively, it would seem that it should be the other way around. Have I made an embarrassing math error, or is there something here that I’m missing?

2

I don’t think you’re missing anything. The math appears to check out, up to maybe some significant figures.

It’s worth noting that rather than ‘g’, escape velocity is more relevant. And from Earth’s orbit, velocity to escape the Sun is a bit less than 4 times the velocity to escape Earth from Earth’s surface. So, purely from gravitation, the Sun should produce a greater time dilation effect (noting that in practice, we’re subject to other forces).

Acceleration due to gravity follows inverse-squared, while the time-dilation is inverse square root, i.e. the time dilation effect falls off much more gently than acceleration due to gravity.

3

It is not the gravity that you feel, but how deep you are in the well.

For instance, if you decided to do some extreme spelunking under the surface of the Earth, time dilation would keep increasing.

As you get closer to the center, the gravity that you feel will decrease, as it works out that it is only the sphere beneath you that pulls down, everything above cancels out.

In the center of the Earth, you’d feel no gravity at all, but time dilation would be at its maximum.

4

What about the opposite case, where someone is in orbit around the earth?

The person at the center of the earth feels no gravity, because the earth is pulling in all directions equally. His velocity, from a point of reference outside the solar system, is equal to that of the earth. The person in orbit feels no gravity, because his free fall cancels the effect. I don’t know enough to figure out how much his velocity might be, but I’m pretty sure that his velocity (or should I say acceleration?) is much more than the guy at the center of the earth.

5

Time dilation depends on how deep you are in a gravity well. Relevant XKCD diagram

The gravitational field you feel at the surface is analogous to how steep the edges of that hill are (or rather, would be, if that diagram were to scale on the horizontal axis as well as the vertical). You can be on a steep slope and yet in only a very shallow pit, or on only a very gentle slope, far down in a deep pit.

6

A person in orbit is affected by gravity, just as you would be affected by gravity while falling off a cliff.

It is just that they are moving quickly enough that they pass the horizon before they hit it.

The don’t “feel” gravity because everything is falling together.

LEO is still 90+% gravity of the Earth.

This is something that has to be taken into account for GPS satellites. It does turn out that the effect of the decrease in gravity is greater than the increase in velocity, and so they run slightly faster than a ground based clock.

7

8

Wait, we can do LaTeX here? How’d you do that?

9

I had no clue either, but try quoting Strangelove’s post & you’ll see how it’s done.

In summary: There’s some website somewhere where you can feed a LaTex string into their url parameters and it’ll send back the corresponding dynamically generated graphic. When you put that fancy url into Discourse, the graphic is displayed to the folks reading your post.

Your second paragraph is one of those truly superb pithy explanations that comes only from folks who a) really know their stuff, and b) really know how to teach. Thank you!!

10

Thanks to all for the help. Conceptualizing it as depth vs. slope helped a lot.

11

Note that the GPS satellites have to take into account the fact that the time dilation in orbit is ever so slightly less than here on earth and that if it didn’t the readings would drift by over 10 km per day. I haven’t calculated at what decimal place the difference lies, but it does illustrate how precise these timings have to be.

12

I had to pull a few tricks to get it working. Discourse only renders a URL as an image if it ends in a picture extension like .jpg or .png. I had to put a hidden string at the end of the LaTeX so Discourse would detect it. I also had to do some manual URL encoding since Discourse has some bugs in the way it detects URLs. All in all, it’s not yet worth it. I’m trying to get the board to support the MathJax plugin, which would give native support, but with the admin side of things still in chaos I doubt it’ll happen soon.

13

I am a dev, and know what LaTeX is about, but don’t know LaTeX syntax.

I took one look at all that escaping and nested mess and said to myself: “I give our good Dr. S high marks for persistence. By Golly he’ll make it work no matter how long it takes!”

Yeah, not a trick ready for use by the general population of SDMB math geeks. At least not until MathJax.

But the next time I need help deciphering a long regex I know who I’m gonna call.

14

Note that you can have the gravitational time dilation between two observers who are feeling the same gravitation acceleration. This fact turns up for the case of an infinite plane (the gravitational force 1 mile above the plane is exactly the same as the force on someone standing on the plane) - or more plausibly for two people at different points on an accelerating object. For a rocket accelerating at 1 g, the guy near the exhaust is aging at a different rate than the guy at the pointy end, even though they are feeling the same acceleration.

15

I’m not sure that I follow. I’ve not heard this before.

Wouldn’t that violate the equivalence principle?

We are assuming an otherwise empty universe, so no other gravitational fields in play, right?

16

I don’t think this violates the equivalence principle - the dilation occurs when one guy is in a different potential than the other regardless of whether the potential is due to gravity or acceleration. All I’m saying is an elaboration of what Chronos said - the dilation is due to the deepness of the well (potential), not the acceleration (slope), even in the extreme case where the slope is identical.

17

But acceleration doesn’t actually create a gravity well, it just feels as though it does.

For sufficiently small regions of space-time, one is indistinguishable from the other, but in the macro universe, they can be. And of course, time dilation is meaningless in a sufficiently small space that you can only fit one clock. You need to be able to compare two different clocks in order for it to be meaningful.

If you are on a rocket, and you want to tell if you are on the Earth or in space under thrust, you can measure the difference in gravitational force between your head and feet. In a rocket, they will be identical, on Earth, with good enough equipment, they will differ slightly.

The same with time dilation. On Earth, a clock at your feet is going to run more slowly than a clock over your head. What you are saying is that this is also the case under acceleration?

This is the first time I’ve ever seen that two observers being accelerated uniformly would experience different time dilation, based on their location orientated to the acceleration.

Equivalence principle would say that if they are undergoing the same acceleration, then they would be undergoing the same time dilation.

Or is it that they are somehow not being accelerated uniformly?

I am very curious about this, as it is a new concept for me that potential energy would make a difference. I guess as you lift an object from a lower point to a higher point in the accelerating rocket, that is increasing its potential energy, as you have to put in work to do so, and could get work out if you let it drop. In the process, you have different accelerations as well, but it seems they would balance out when it came to a stop.

It seems if that is to be the case, though, the higher object has the higher potential energy, and as such, should actually be running slower than the lower object.

I’m not sure how the act of accelerating creates a gravitational potential well for you to be higher or lower in.

In the case of accelerating, time dilation is directly related to the acceleration you are undergoing, unlike gravitational acceleration, where it is dependent on your depth in a gravity well, and is no dependent on your acceleration.

Also, in a gravity field, you are running slower. In an accelerating frame, you are slowing down.

Could you explain further or link to some literature that does?

18

You can contrive an arrangement of masses such that the gravitational acceleration is uniform over some small area. Put a tower in such a gravitational field, and the clock at the bottom of the tower still runs slower than the one at the top (because it’s at a lower potential). The rocket does the same thing as the tower, and so the equivalence principle holds.

And @Andy_L, you can sort of get away with talking about an infinite plane of mass in Newtonian gravity, but once you’re doing GR, it’s nonsensical. For one thing, since the mass within any radius is proportional to the square of the radius, there will be some maximum radius beyond which your slab of mass will collapse into a black hole.

19

That’s weird.

So, both clocks are slowing down wrt an outside observer, but the one in the front is slowing down less than the one on the bottom?

Would the dilation between the two clocks stay the same? One is .0001% faster than the other, and it is still the case next year (assuming you can keep your acceleration up that long), or would the one on bottom keep slowing down more and more relative to the upper one?

I assume the former, but an hour ago I would have assumed that they were both the same, so what do I know?

I’ll need to spend some time wrapping my brain around that one.

20

Yeah. You’re right. Instead of an infinite plane, consider a very large but finite plate. At the center of the plate, for vertical distances small compared with the radius of the plate, gravitational force is very nearly constant.