ISWYDT. 
[As one would expect for this strip, turns out it’s a 100% bone dry gag based on a very obscure term and some funky geometry.]
Come on, don’t be such a
(and if you think that’s a rectangle not a square, then get your head out of Euclidean space, man)
I’ve long observed that the smaller the set of people who get a joke, the funnier it is to that set of people. So a joke that’s only understandable to nerds is hilarious to nerds, even as it falls completely flat for everyone else. And the absolute funniest jokes are in-jokes that are only gotten by 2 or 3 people.
Nope, I’ve got no idea.
Or… we are washed-ups or wannabes that look it up and get a brief hit of insight or joy.
The Exploratorium and San Francisco were a fun part of my history @ 45 years old.
Ditto. I sometimes learn stuff from the comments on this thread, but a lot of the time the cartoon and the comments just go over my head. I keep following it because I do learn stuff, which I appreciate.
Simplifying mightily …
An catenary is a mathematical description of a particular regular, but not circular, curve. Typically they’re convex downwards and concave upwards. An “inverted” catenary is the opposite: same shape but convex upwards.
So you could build an undulating surface of adjacent inverted catenary bumps, looking something like a straight line of small waves progressing across a pond.
One of the weird features of a catenary curve is that a square wheel will roll smoothly on that surface. Or said another way, if you tried to roll a square wheel on a flat surface, the corners would describe catenary curves as they rotate. So the funky way a square wheel rolls is exactly offset when rolling on the matching funky surface: an inverted catenary. The square wheel rolls smoothly across that surface, just like a round wheel does on a flat surface.
From there the joke connects to the current changing of the seasons and the falling of snow signaling it’s time to put on your snow tires. Once it’s catenary curves falling from the sky, time to put on your square tires. So you can roll smoothly on the resulting undulating roads covered in catenary bumps.
The museum of mathematics in NYC used to have a room with a but circle in the middle covered with reverse catenary curves, and tricycles with square wheels you could ride over it.
“Luckily, the range is limited by the fact that the square boundary lines follow great circles.”
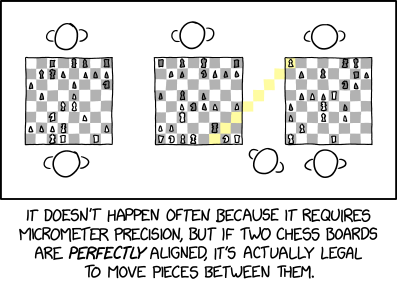
Without checking, I imagine some nerd over at explainxkcd has already calculated the max range before a great circle around the Earth differs from a straight line by more than a micrometer.
I wonder which “square boundary lines” he’s referring to and why he thinks any of them follow great circles?
Assuming a geometrically ideal chessboard, no portion of it follows a great circle. Assuming they’re placed on a geometrically ideal table, that too will be planar, not great circle.
Obviously there is an upper limit to the size of a truly planar table in the real world. A table a few miles long would not be perpendicular to the local gravity gradient at either end, and at some length a table that’s e.g. 30" above the floor at each end would touch the curved surface of the Earth at its midpoint. Assuming an idealized smooth (but not necessarily spherical) Earth.
So many rabbit holes to explore. So little motivation to do so.
Yeah, this one was pretty weak. Especially since there’s no particular reason for the precision required to be micrometer, rather than millimeter or nanometer. I mean, on a typical-sized chess board, I’d accept misalignments on the order of millimeters within the board itself as tolerable.
Of course the real motivation for the tolerance is to make the occurrence so rare that none of us has ever heard of it, much less seen it. Millimeters would flunk the unexpected test. Which is an essential element of humor. Even weak humor.
So many times I’ve been so enraptured by an XKCD where I happen to be in the small class of people who get the reference that, no matter how irksome it might be, I have to forgive Randal for the ones some other small class gets that I haven’t any idea about.
That’s the point, that the ideal straight line does not follow a great circle. It deviates, and at 3.57m away from the tangent point, it deviates by more than a micrometer.
So did you do the calc, or find it already done by somebody else over at explain? 
Yes, I get that great circles are not straight lines. And therefore the two lines would spread apart as you travel along both lines from a common starting point.
My objection was Randall said “by the fact that the square boundary lines follow great circles.” The square boundary lines (whatever specifically those are), don’t follow great circles. If they did there’d be no divergence.
Or else I just don’t understand what he’s trying to say. Which is certainly possible. Even if you choose to extend the edges of both boards along great circles, not straight lines, then they’d be perfectly aligned by that definition when they both lie on the same great circle.
I totally get the idea he was aiming for. IMO he failed to express it accurately. Which is in fact quite difficult to do in the small number of words that make a good hover-over.
Straight lines would neither converge nor diverge. Great circles do not diverge, but do converge. Take any two “parallel” great circles on the Earth’s surface, and they’ll converge a quarter of the Earth’s circumference away.