Yes. Especially if your passenger says things like, “watch out, there’s a car coming from the left”.
Almost all people have more than the average number of legs
Between 1997 and 2007, the average MLB pitcher had more than 10 fingers.
Not in 1997-1999, when Jim Abbott was pitching.
Good catch (heh). I guess Bob Wickman also threw off the numbers a bit.
“Anyone else watching this Youtube video in 1954? If so, my last trip definitely messed with the timeline.”
Now that, I liked.
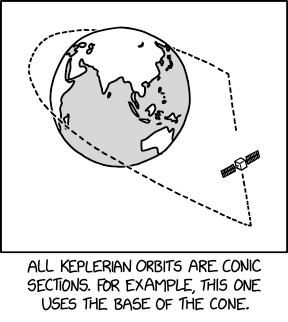
“They’re not generally used for crewed spacecraft because astronauts HATE going around the corners.”
Well, off to explainxkcd.com. I don’t get this at all.
Crewed spacecraft don’t really worry about going around the corners because those don’t come back.
Different take than @DesertDog …
There are a lot of different conic sections. a circle, an ellipse, and a hyperbola are all legit orbits which are also conic sections. But there’s an implicit bit in the term “conic section” that your cone is infinitely tall. IOW, it does not have a base.
If you take a real physical non-infinite cone, it does have a base. And if you cut a cone with a plane oriented such that it penetrates the base, the result is a smooth curve that’s sort of half an orbit, with two square corners at the bottom, and a straight line between the square corners.
Any vehicle that tried to follow that sorta-conic section path would experience infinite G-forces as it negotiated the square corners. Which experience would convert astronauts into ketchup. Hence unpopular.
Yes, it’s a joke about the difference between mathematical conic sections and sections of an actual, finite cone, like an ice cream cone.
One valid conic would be traveling in a straight line away from the gravity source forever.
If it followed an imaginary path, would that be iConic?
Booo! *throws tomato*
I think we should throw ice cream cones instead. Filled with something noxious, not yummy ice cream.
As one of my math teachers noted, each of those terms has a counterpart in the field of rhetoric: you can speak hyperbolically, or elliptically, or relate a parable, or talk in circles. (Or make a few points to form a line of argument…)
If I told you that a particular curve had an eccentricity of, like, a million, that would be a hyperbole.
That’s what I implied by, “It doesn’t come back,” – no shortcut across the base of the cone.
Well, hard to tell from a hand-drawn illustration. Any conic section other than a circle could intersect with the base.